問題(速さの問題)
|
|
|||
|
|
 |
兄と妹の2人が家の近くの公園までの道のりを、それぞれ一定の速さで歩いて往復します。 兄は妹よりも5分遅れて出発しましたが、出発してから10分後に公園までの道のりの3分の1の地点Aで妹を追い抜きました。 妹は、出発から何分歩いたところで公園を引き返してきた兄と出会うことになりますか。 |
|
|
|
|
||
解答例1[Aまでの距離を30として、時間の逆比=速さの比]
| TORAさん、maruhagedonさん、ねこやんさん、洋輝さん、
トトロ@Nさん、スモークマンさん、千鶴。さん、takamatsuさん、数楽者さん、
ヒデー王子さん、hiroさん、ひろさん、ヨッシーさん、
小杉原 啓さん、AIRさん、nikonikoさん、パリンさん、きっちょむさん、 tomhさん、算数題魔人さん、つる太さん、チュパさん、三木さん、 BossFさん、他 |
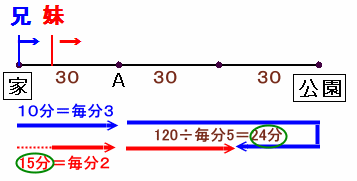
家からAまでの距離を30とします。
兄はこれを10分で歩くので、30÷10=毎分3、
妹はこれを15分で歩くので、30÷10=毎分2 の速さとなる。2人は追いこしのあと、2人合わせて30×4=120だけ進んだところで出会うから
120÷(3+2)=24分後に出会う。
妹から見て、これは出発から15+24=39分後のことである。答 39分
以上
解答例2[小刻みに分けて、A迄の距離仮定/兄の往路復路場合分け、ダイヤグラムを描いて]
| 辻。さん、有無相生さん、ふじさきたつみさん、きよたんさん、まるケンさん、
GROMITさん、ほなみさん、BEANさん、ちょみやさん、 わにがわさん、C-Dさん、USKさん、 長野美光さん、まおさん、テモさん、とらいしくるさん、他 |
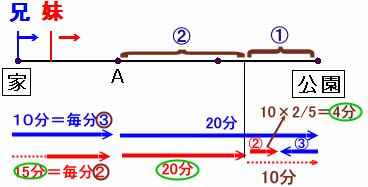
兄と妹の速度比が3:2であることは解答例1と同様。
兄は家からA地点まで10分かかるので、A地点から公園までは距離が2倍なので10×2=20分、合計30分かかります。
兄が公園に到着したとき、妹はA地点からは20分歩いているので、公園まであと10分の地点にいます。
この距離を兄:妹=3:2の速度比で分けると、妹の所要時間は10分×2/5=4分。
従って、家を出発してからは、15+20+4=39分歩いています。
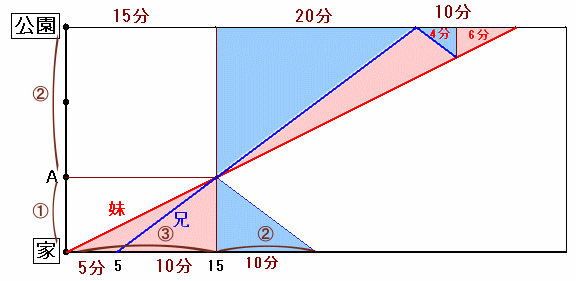
これをダイアグラムで表すと、下図のようになります。
解答例3[二人の速さを合わせると18分かかるので]
| ミミズクはくず耳さん、kunioさん、他 |
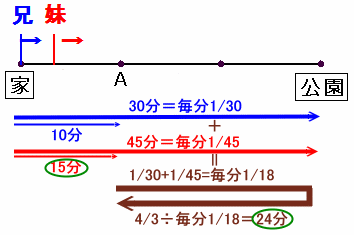
家からA地点までの所要時間:兄は10分、妹は15分
家から公園までの所要時間(距離が3倍):兄は30分、妹は45分。従って、家から公園までの距離を1とすると、
2人の速さ合計=1/30 + 1/45 = 1/18
となり、2人合計だと所要時間は18分となります。A地点から2人が次に出会うまでに、2人合わせて2/3×2=4/3の距離を進むので、
4/3×18=24分かかります。したがって、妹が歩き出してからでは、15+24=39分になります。
(その他の解法)
- 方程式で解く ・・・ 大岡 敏幸さん、A.NOUCHIさん、mhayashiさん、他