問題(空間図形)
|
|
|
|
|
|
|
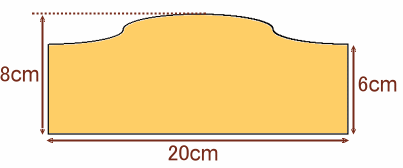 |
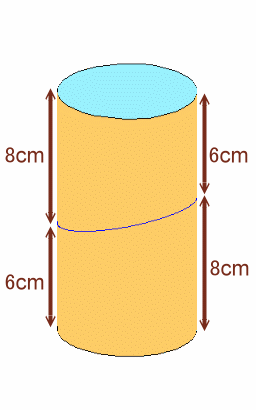
左図は円柱形の筒を、平面で切断したときにできる立体の側面の展開図です。 この展開図の面積は何cm2ありますか。 |
|
|
|
|
|
|
解答例1[高さ14cmの円筒の半分 、高さ7cmの円筒と比べて、高さ8cmの円筒と6cmの円筒の中間値]
| TORAさん、Banyanyanさん、トトロ@Nさん、Taroさん、ヌオさん、
C-Dさん、まりまりさん、まりまりさん、あまれっとさん、maruhagedonさん、
まるケンさん、まこさん、N.Nishiさん、ねこやんさん、
大岡 敏幸さん、GOMAさん、娘。さん、takamatsuさん、数楽者さん、
つる太さん、takahiroさん、クララさん、BEANさん、智ベン和歌山さん、
智ベン和歌山さん、やまけんさん、西 信好さん、TOMOKIさん、道家 尚秀さん、
信三さん、 ミミズクはくず耳さん、Nの悲劇さん、
きっちょむさん、TOMOKIさん、とっしーさん、 他 |
[アニメON]を押すと円筒が回転するようすをアニメで表示します。
題意より、展開図を組み立てた立体を2つ重ねると、高さ14cmの円筒にな り、この側面の展開図は、高さ14cm、幅20cmの長方形となります。
求めるものは、この半分の立体の側面積だから
20×14÷2=140cm2答 140cm2
以上
解答例2[展開図を等積変形 、山型の部分=20x2/2]
| mhayashiさん、勝浦捨てる造さん、ながちゃんさん、永嶋 幸司さん、mkuraさん、
A.NOUCHIさん、長野美光さん、tekiさん、ふじさきたつみさん、ヒデー王子さん、
文花さん、ごまちゃんさん、tomhさん、ちょみやさん、AIRさん、
Feroさん、 ほなみさん、パリンさん、マッスルさん、エオウィンさん、スモークマンさん、 kobaさん、とらいしくるさん、HAJIさん、HAJIさん、耕平さん、 USKさん、松嶋和美さん、他 |
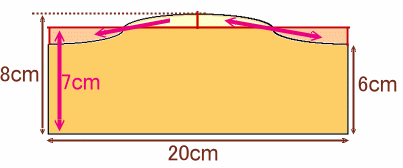
円柱の側面を平面で切断すると、断面は円を斜めに引き延ばした形(楕円)になります。
したがって、展開図の凸になってる部分を2分割し、その左右の凹になってる部分に移動すると、縦7cm、横20cmの長方形 になります。
従って、求める面積は、7×20=140cm2
(その他の解法)
- 積分で ・・・ 有無相生さん、 他