問題(平面図形)
|
|
|
|
|
|
|
 |
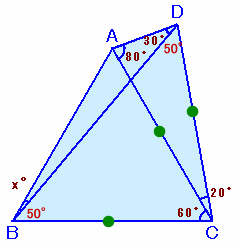
左図で、∠ACB=60度、∠ACD=20度、∠CAD=80度、∠ADB=30度です。 では、∠ABDは何度ですか。 |
|
|
|
|
|
|
解答例1[ 2つの二等辺三角形と1つの正三角形]
| ふじさきたつみさん、コダックさん、勝浦捨てる造さん、あああああさん、ながちゃんさん、 永嶋 幸司さん、マッスルさん、ミミズクはくず耳さん、C-Dさん、maruhagedonさん、 N.Nishiさん、智ベン和歌山さん、大岡 敏幸さん、あまれっとさん、つる太さん、 Banyanyanさん、ヒデー王子さん、ごまちゃんさん、Taroさん、Nの悲劇さん、 HAJIさん、ステップ ばい ステップさん、mhayashiさん、フランク長いさん、AIRさん、 GOMAさん、パリンさん、ほなみさん、熱狂的巨人ファンさん、ねこやんさん、 tomhさん、mikiさん、TOMOKIさん、ヨッシーさん、まるケンさん、数楽者さん、翔太のパパさん、トトロ@Nさん、有無相生さん、 スモークマンさん、長野美光@インドネシアさん、takedaさん、1ゆりさん、たけさん、 土橋 雅樹さん、きっちょむさん、tekiさん、emikoさん、MAIさん、 chihayaさん、とらいしくるさん、修平さん、BossFさん、岡崎さん、 他 |
上田さんと下田さんの答案を比べて見ます。
△CDAと△CDBが二等辺三角形でCDが共通で、角ACB=60度だから、△ABCは正三角形。<br>したがって、x=60−50=10度:
△CADと△CBDが二等辺三角形から、CA = CB<br>で、頂角が60度だから、∠ABC = (180-60)/2 = 60<br>したがって、∠ABD = 60-50 = 10<br>やり方はいっしょですが、△ABCが正三角形は意識しないで解いてしまいました。:
答 10°
以上
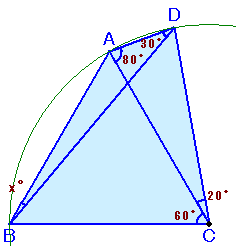
解答例2[円の中心角とかを使った]
| フンガー中山さん、他 |
∠ACB=∠ADB×2より、B、A、Dは点Cを中心とする円周上にあります。
(∠ACB:中心角、∠ADB:円周角)従って、今度は∠ACDが中心角、∠ABDが円周角より、
∠ABD=∠ACD÷2=20÷2=10°と分かります。