問題(時計算)
|
|
|
|
|
|
|
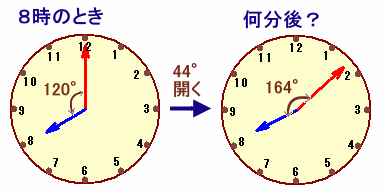 |
ある時計が、ちょうど8時を指しています。 時計の長針と短針の間の角度が初めて164度になるのは、今から何分後ですか? |
|
|
|
|
|
|
解答例1[120度が164度に]
| TORAさん、C-Dさん、鍵谷保奈美さん、origatsuさん、あまれっとさん、 フランク長いさん、bbさん、有無相生さん、きっくさん、maruhagedonさん、 仮面Xさん、ねこやんさん、パリンさん、ながちゃんさん、永嶋 幸司さん、 HEROさん、GOMAさん、数楽者さん、ムーさん、るんたったさん、 Taroさん、熱狂的巨人ファンさん、ヌオさん、翔太のパパさん、スモークマンさん、 とらいしくるさん、Banyanyanさん、あほさん、長野美光さん、HAJIさん、 マッスルさん、あああああさん、ミミズクはくず耳さん、BossFさん、GROMITさん、 増島裕紀さん、tekiさん、tomhさん、算数題魔人さん、ウッキー・タクヤさん、 ありささん、芳田 啓輔さん、takamatsuさん、すぴおさん、]]さん、 トトロ@Nさん、松尾芭蕉さん、あやっちさん、Capt.さん、iinoueさん、 チュパさん、トシえもんさん、ばつさん、他 |
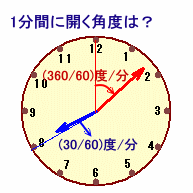
長針と短針の間が1分間に開く角度を求めてみましょう。
長針:1時間(60分)に1回転=360度、360÷60=6度/分
短針:1時間(60分)に1/12回転=360度÷12=30度、
30÷60=0.5度/分従って、6−0.5=5.5度/分の割合で開くことになります。
8時の時点で長針と短針の間は120度開いていますから、164度になるには、あと164−120=44度だけよけいに開くことになります。
従って、44度÷5.5度/分=8分後 となります。
答 8分後
以上
解答例2[1時間で330度だから]
| Banyanyanさん、他 |
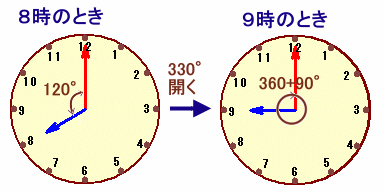
1時間後を考えてみましょう。。
9時には、長針は短針を1度追い越しますので、間は360+90=450度開いていることになります。
従って、1時間(60分)の間に、450−120=330度だけ開きが増すことになるわけです。
164−120=44度だけますには、60分×44度/330度=8度と分かります。
(その他の解法)
- 方程式を用いて解く ・・・ 辻。さん、mhayashiさん、クララさん、大岡 敏幸さん、N.Nishiさん、 たつみさん、悠さん、evolutionさん、A.NOUCHIさん、takedaさん、 他