問題(平面図形)
|
|
|
|
|
|
|
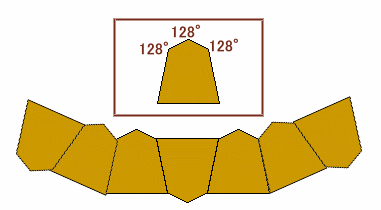 |
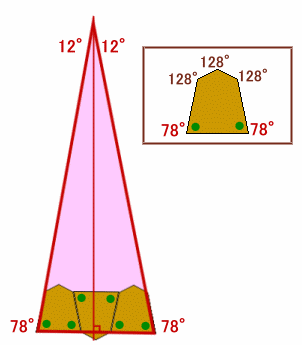
枠内の図のような、左右対称形をした五角形の板がたくさんあります。 この板を、下上上下上上下上上・・・・・と、一定の規則で隙間の無いように並べていきます。 板が1周ぐるっと廻って大きな円となるためには、この五角形が何枚必要ですか。 |
|
|
|
|
|
|
解答例1[上下上を1組にして]
| TORAさん、mhayashiさん、信三さん、辻。さん、オリガツさん、 Mの喜劇さん、Banyanyanさん、たつみさん、犬飼仁史さん、長野美光@インドネシアさん、 あまれっとさん、トトロ@Nさん、とらいしくるさん、あああああさん、 数楽者さん、ミミズクはくず耳さん、勝浦捨てる造さん、フランク長いさん、じゅうたん島さん、 ありささん、GOMAさん、るんたったさん、ヌオさん、AIRさん、 ゾロさん、N.Nishiさん、ステップ ばい ステップさん、有無相生さん、鈴木さん、 鍵谷保奈美さん、Nの悲劇さん、ponta55555さん、Taroさん、tekiさん、 AZUKUNさん、A.NOUCHIさん、tomhさん、とりやまさん、かあさんさん、 トシえもんさん、大岡 敏幸さん、こざっぱさん、tanikawaさん、白須大樹さん、 ねこやんさん、こうちゃんずさん、めそさん、パリンさん、他 |
まず、五角形の底角を求めます。
五角形の内角の和=180×(5−2)=540°だから、
底角=(540−128×3)÷2=78°
となります。上下上を1組にして考ると、
下向き五角形の底角と上向き五角形の底角は等しいので、3つの底辺は平行。従って、両側の上向き五角形の底辺は一直線上に並びます。
これを結んだ線分を底辺とし、上向き五角形の斜辺に重なるような二等辺三角形を考えると、
頂角=180−78×2=24°になります。360÷24=15なので、これらを15組を並べるとちょうど1周することになります。
板は1組3枚なので、合計=3×15=45枚となります。答 45枚
以上
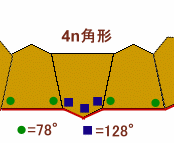
解答例2[4n角形の内角の和を考えて]
| 高橋 道広さん、他 |
解答例1と同様、上下上を1組にして考えて、全部でn組あるとします。
3n枚の板の外側の辺でできる4n角形の内角の和=180×(4n−2)度。
3枚分の内角の和=78×4+128×3=696度。従って、
180×(4n−2)=696×n、
24n=360
よって、n=360÷24=15。よって、板の合計枚数=15×3=45枚となります。
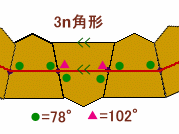
解答例3[ 斜めの辺の中点を結ぶ]
| C-Dさん、他 |
やはり、上下上を1組にして考えて、全部でn組あるとします。
五角形の斜辺の中点を次々に結んでできる3n角形の内角の和=180×(3n−2)度。
3枚分の内角の和=78×4+102×2=516度。従って、
180×(3n−2)=516×n、
24n=360
よって、n=360÷24=15。よって、板の合計枚数=15×3=45枚となります。