第４４問の解答

問題（ 規則性、場合の数）

1,3,5,7,9を使わないで出来る整数を、小さい方から順に書き並べます。

2、4、6、8、20、22、24、26、28、40、42、44、・・・

2002は、この数列の何番目に出てきますか？

解答例１［変則５進法で］

N.Nishiさん、高橋　道広さん、Nonさん、長野　美光さん、HAJIさん、 信三さん、ヒデー王子さん、tomhさん、たつみさん、トトロ＠Ｎさん、 栗原英治さん、鍵谷保奈美さん、数楽者さん、ねこやんさん、フランク長いさん、 大岡　敏幸さん、kudahさん、POIさん、航介さん、他

参考図１

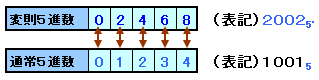
数字の０、２、４、６、８をそれぞれ０、１、２、３、４と置きなおすと５進数と１：１に対応させることができます。そこで、このような数を変則５進数と呼び、２００２5'のように表すことにします。

２００２5'は、１００１5＝１×５3＋０×５2＋０×５1＋１×５0＝１２６と対応します。
従って、２００２は１２６番目に出て来ることが分かります。

答　１２６番目

以上

解答例２［書き出し！ 、10X10の桝目を使って］

TOMOKIさん、C-Dさん、ながちゃんさん、永嶋　幸司さん、勝浦捨てる造さん、 AZUKUNさん、翔太のパパさん、釣り弟子さん、あまれっとさん、マッスルさん、 トシえもんさん、暁菜さん、ミミズクはくず耳さん、ヌオさん、Ｍの喜劇さん、 TATSUKIさん、わにがわさん、A.NOUCHIさん、犬飼仁史さん、とらいしくるさん、 ばつさん、　USKさん、他

参考図２

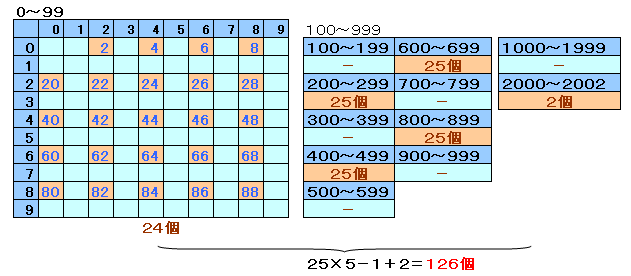
桁数で場合分けして数え上げると、
　２４＋２５×４＋２＝１２６通り
となります。

解答例３［4桁になって2番目の数字ゆえ、 重複順列、場合の数］

ＴＯＲＡさん、Taroさん、maruhagedonさん、辻。さん、有無相生さん、 AIRさん、るんたったさん、オリガツさん、Banyanyanさん、まおさん、 hukuさん、emikoさん、takuさん、tekiさん、 　VILLさん、　ryo sagawaさん、他

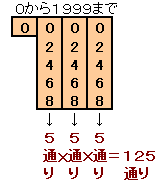
００００〜１９９９までを考えてみます。

参考図３

  • 先頭の数字：０のみ　・・・　１通り

  • ２番目の数字：０、２、４、６、８　・・・　５通り

  • ３番目の数字：０、２、４、６、８　・・・　５通り

  • ４番目の数字：０、２、４、６、８　・・・　５通り

よって、５×５×５＝１２５通り。

これから、００００を除き、２０００、２００２を加えて、
合計＝１２５−１＋２＝１２６通りとなります。

（その他の解法）