第４６問の解答

問題（平面図形）

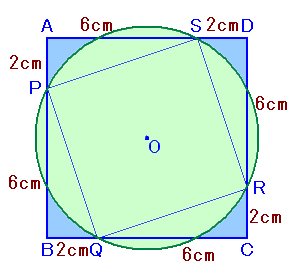左図の四角形ABCDは、1辺が8cmある正方形で、
P、Q、R、Sは、この正方形の各頂点から2cmの場所にあります。

4つの点P、Q、R、Sを通る円Oの面積は何cm²ありますか。

解答例１［半径×半径を表わす正方形を探す、円：内接正方形＝3.14：2］

ＴＯＲＡさん、Taroさん、Banyanyanさん、江端ちはやさん、maruhagedonさん、小杉原啓さん、ヌオさん、あまれっとさん、鍵谷保奈美さん、高田修成さん、 AIRさん、ねこやんさん、数楽者さん、パリンさん、たつみさん、あああああさん、Nの悲劇さん、HAJIさん、長野　美光さん、TOMOKIさん、 sizukaさん、トトロ＠Ｎさん、仮面Xさん、お願い聞いてさん、おーｃ算数大好きさん、 MaskMan2さん、　C-Dさん、hukuさん、ミミズクはくず耳さん、他

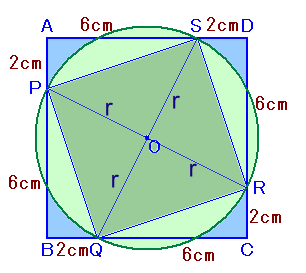
円Oの半径の長さをrとします。

　正方形PQRSの面積＝r²×２
＝正方形ABCDの面積－△APD×４
＝８×８－1/2×２×６×４
＝４０cm²

よって、r²＝２０cm²。

　円Oの面積
＝π×r²＝３．１４×２０
＝６２．８cm²

　

答　６２．８cm²

以上

解答例２［素直に三平方の定理］

有無相生さん、tekiさん、tomhさん、るんたったさん、トシえもんさん、 mhayashiさん、yukiさん、大岡　敏幸さん、BEANさん、 N.Nishiさん、きょえぴさん、とらいしくるさん、勝浦捨てる造さん、ながちゃんさん、スモークマンさん、白須大樹さん、A.NOUCHIさん、GOMAさん、釣り弟子さん、ふじいさん、他

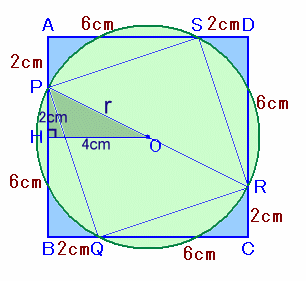
円の中心OからABに下ろした垂線の足をHとします。

△PHOは直角三角形だから、
r²＝PH²＋OH²
　＝２²＋４²
　＝２０

よって、　
円Oの面積
＝π×r²＝３．１４×２０
＝６２．８cm²

解答例３［強引に半径を出す］

辻。さん、熱狂的巨人ファンさん、翔太のパパさん、わにがわさん、ヨッシーさん、他

△SAPは直角三角形だから、
SP²＝AP²＋SA²
　＝２²＋６²
　＝４０

よって、SP＝√４０cm。

△SPOは二等辺直角三角形だから、
　ｒ＝OP＝SP÷√２＝√４０÷√２＝√２０

円Oの面積
＝π×r²＝３．１４×２０
＝６２．８cm²


	円の中心OからABに下ろした垂線の足をHとします。 △PHOは直角三角形だから、 r²＝PH²＋OH² 　＝２²＋４² 　＝２０よって、　円Oの面積＝π×r²＝３．１４×２０＝６２．８cm²


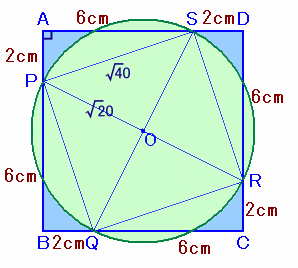
	△SAPは直角三角形だから、 SP²＝AP²＋SA² 　＝２²＋６² 　＝４０よって、SP＝√４０cm。 △SPOは二等辺直角三角形だから、　ｒ＝OP＝SP÷√２＝√４０÷√２＝√２０円Oの面積＝π×r²＝３．１４×２０＝６２．８cm²