問題[場合の数:最短経路]
|
|
|
|
|
|
|
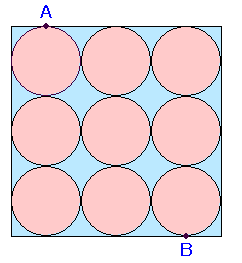 |
左図のAからBまでを、最短距離で進みたいと思います。 道順は何通り考えられますか? |
|
|
|
|
|
|
解答例1[普通に、1/4回転の組み合わせ]
| 小杉原 啓さん、GOMAさん、るんたったさん、川村さん、BEANさん、 トシえもんさん、ミミズクはくず耳さん、轟さん、数楽者さん、パリンさん、 ponta55555さん、勝浦捨てる造さん、辻。さん、ヨッシーさん、N.Nishiさん、 mhayashiさん、有無相生さん、轟さん、きよたんさん、翔太のパパさん、土橋さん、 大岡 敏幸さん、他 |
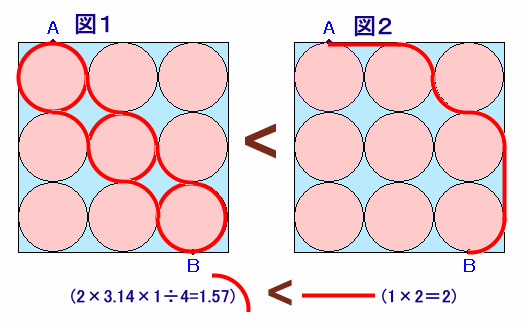
最短経路は図1のように4分の1円6個をたどるものに限られます。
なぜなら、図2のように4分の1円の替わりに半径2個分の直線に置き換えることもできますが、円の半径を1とすると、
4分の1円の長さ=2×3.14×1÷4=1.57
半径2個分の直線=1×2=2
となり、距離が長くなってしまうからです。
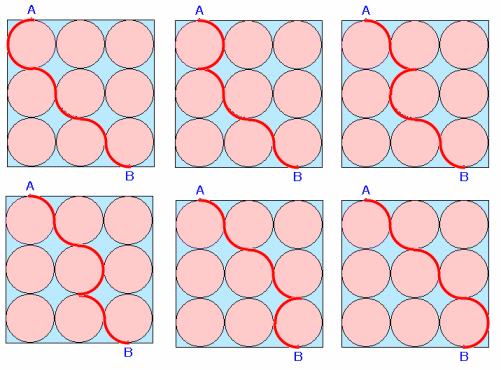
図1の経路から、最短経路を数え上げると、上図のように6通りとなります。
答 6通り
以上
解答例2[はしごに直して、○5つと×1の並べ替え]
| maruhagedonさん、C-Dさん、まるケンさん、川村さん、 お引越しさん、tomhさん、hukuさん、Nの悲劇さん、Taroさん、 長野美光さん、轟さん、evolutionさん、あああああさん、AKAさんさん、 たつみさん、AIRさん、トトロ@Nさん、フランク長いさん、航介さん、高橋 道広さん、他 |
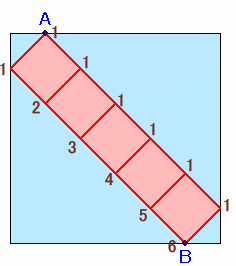
解答例1の図1より4分の1円を直線に直すと、下図のような5×1の格子上最短経路に置き換えることができます。
すると、6個ある左斜め下方向の道のどれか1つだけ進むことができるので、合計6通りになります。
一般に、n×mの格子上最短経路数は、n+mCn通りとなります。