問題[整数の性質]
|
|
|
|
|
|
次の あ〜かに1から6までの整数を1個ずつあてはめて、式が成り立つようにして下さい。
|
|
|
|
|
|
解答例1[条件より絞りこむ]
| やまけんさん、パリンさん、あああああさん、他 |
[{(10+あ)×い+う}×え+お]×か
=(10+あ)×い×え×か+う×え×か+お×か
=100
より、 い×え×か<10でなければならない。よって、あ〜か=1〜6なので、(い、え、か)=(1、2、3)、(1、2、4)のどちらか となります。
また、(い、え、か)に1、2とも含まれるので、あ≧3となり、
(10+3)×8>100
なので、(い、え、か)=(1、2、4)は不適。よって、(い、え、か)=(1、2、3)、(あ、う、お)=(4、5、6)。
すると、あ×6+(う×え+お)×か=100−10×6=40となり、
あ×6≧4×6=24、う×え+お≧4×1+5=9なので、
もし、か≧2なら、左辺=24+9×2≧42となり不適。
よって、か=1。すると、え≧2となるので、う×え+お≧4×2+5≧13となり、
もし、あ≧5なら、左辺≧5×6+13≧43となり適。
よって、あ=4。従って、う×え+お=40−4×6=16となり、
また、う、お≧5、え≧2なので、
もし、え≧3なら、左辺≧3×5+5=20となり不適。
よって、え=2。(い、え、か)=(1、2、3)で、え=2、か=1と決まったので、残った、い=3。
(あ、う、お)=(4、5、6)で、あ=4と決まったので、(う、お)=(5、6)う×2+お=16となり、おは偶数でなけれなならないので、
お=6、う=5。以上より、あ=4、い=3、う=5、え=2、お=6、か=1となります。
答 あ=4、い=3、う=5、え=2、お=6、か=1
以上
解答例2[ 答を最小にする]
| とらいしくるさん、鍵谷保奈美さん、としおとこさん、他 |
和=[{(10+あ)×い+う}×え+お]×か の値を最小に するように考えます。
い×え×か≧え×か≧か で 、10+あ>う、え なので、
い×え×か をできる限り小さくする必要があるので、
い×え×か=1×2×3。同様に、え×か、および か もできるだけ小さくする必要があるので、
え×か=1×2、 か=1
従って、い=3、え=2、か=1と考えられる。すると、
和=(10+あ)×6+う×2+お=あ×6+う×2+お+60
(あ、う、お)=(4、5、6)なので、あ、う、お は小さい順にするのがよく、
よって、あ=4、う=5、お=6と考えられる。このとき、和=4×6+5×2+6+60=100
したがって、和=100となるのは、
あ=4、い=3、う=5、え=2、お=6、か=1
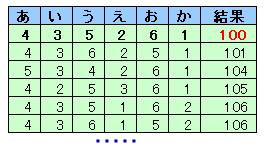
と考えられる。実際、EXCEL等のプログラムで計算し結果を小さい順に並べると下図のようになります。
(その他の解法)
- プログラムで計算 ・・・ mhayashiさん、Taroさん、他
- カード利用 ・・・ TOMOKIさん、 他