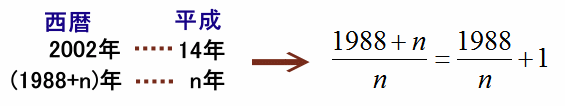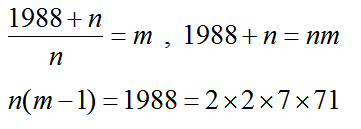問題[整数の性質]
|
|
|
|
|
|
2002年(平成14年)は、2002÷14=143というように、西暦の数字を平成の数字で割ったとき整数の商が求まる年でした。 次に今年と同じように商が整数になるのは今から何年後のことですか? |
|
|
|
|
|
解答例1[西暦と元号の数字の差の約数調べ 、因数を整数にするために]
| Taroさん、maruhagedonさん、Banyanyanさん、C-Dさん、ヌオさん、 トシえもんさん、あまれっとさん、ponta55555さん、フランク長いさん、トトロ@Nさん、 まるケンさん、長野美光@天津さん、ひびき りょうさん、 ねこやんさん、他 |
西暦年と平成年との差は、2002−14=1988なので、
平成n年=西暦(1988+n)年
という関係があります。従って、
西暦÷平成=(1988+n)÷n=1988÷n+1
となるので、西暦年が平成で割り切れるためには、
1988がnで割り切れること、すなわちnが1988の約数となることが必要かつ十分です。1988を素因数分解すると、
1988=2×2×7×71
となるので、1988の約数は、
1、2、4、7、14、28、71、142、284、497、994、1988
と分かります。従って、n>14で最小の約数nは、n=28となりますので、
次に西暦年が平成で割り切れるのは、
28−14=14年後
となります。答 14年後
以上
解答例2[方程式で、不定方程式]
| 有無相生さん、熱狂的巨人ファンさん、大岡 敏幸さん、スモークマンさん、tomhさん、他 |
x年後に、(2002+x)÷(14+x)が、整数mになったとして、
n=14+x とおくと、
(2002+n−14)÷n=m
1988+n=nm
n(m-1)=1988=2×2×7×71よって、
(n、m-1)=(1、1988)、(2、994)、(4、497)、(7、284)、
(14、142)、(28、71)、(142、14)、(284、7)、
(497、4)、(994、2)、(1988、1)n>14なので、n=28が次の年。
従って、x=n−14=14年後となります。
(その他の解法)
- プログラム(EXCELなど)で計算 ・・・ mhayashiさん、SARAさん、二宮金次郎さん、codraさん、ハラギャーテイさん、ふじさきたつみさん、航介さん、他