問題[場合の数]
|
|
|
|
|
|
上図のように、白石と黒石を合わせて8個並べます。 黒石が2個以上続かないように一列に並べる方法は、何通りありますか。 |
|
|
|
|
|
解答例1[フィボナッチ]
| Banyanyanさん、あまれっとさん、C-Dさん、有無相生さん、小杉原 啓さん、 AIRさん、ミミズクはくず耳さん、トトロ@Nさん、ねこやんさん、BEANさん、 カトキチさん、tomhさん、勝浦捨てる造さん、やまけんさん、 ふじさきたつみさん、なかさん、まるケンさん、遼さん、谷本 章さん、 土橋 雅樹さん、他 |
石がn個のときに並べる方法をFn通りとして、漸化式で考えます。
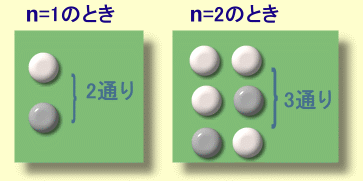
上図のように、 F1=2、 F2=3 で、
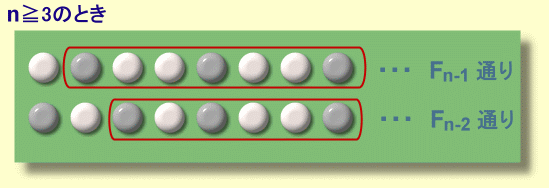
n≧3のときは、
最初の石が白のとき ・・・ 2個目以降は、Fn-1通り
最初の石が黒のとき ・・・ 2個目は白でならなくて、3個目以降は、Fn-2通り
従って、
Fn=Fn-1+Fn-2
が成り立ちます。順次、計算すると、
n 1 2 3 4 5 6 7 8 Fn 2 3 5 8 13 21 34 55 答 55通り
以上
解答例2[コンビネーション]
| N.Nishiさん、ponta55555さん、ヨッシーさん、スモークマンさん、他 |
白石の個数により場合分けして数えます。
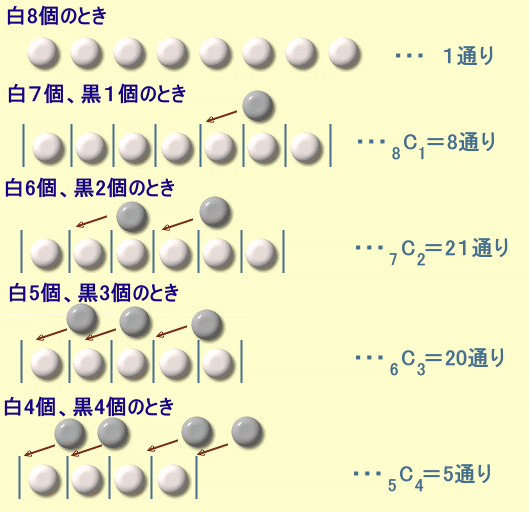
白石ばかり8個のとき ・・・ 1通り
白石がn個のとき、(4≦n≦7)
両端および白石と白石の間、合計(n+1)個の隙間の中から
(8−n)個を選んで黒石を入れる(組み合わせ)ことに相当 ・・・ n+1C8-n通り従って、
合計=1+8C1+7C2+6C3+5C4
=1+ 8+ 21+ 20+ 5
=55通り
となります。
解答例3[重複組み合わせ]
| mhayashiさん、nobuさん、トシえもんさん、長野 美光さん、お引越しさん、 えりぴょんさん、他 |
ほぼ解答例2と同様ですが、黒石をまずおいてから、白石を間に入れることを考えます。
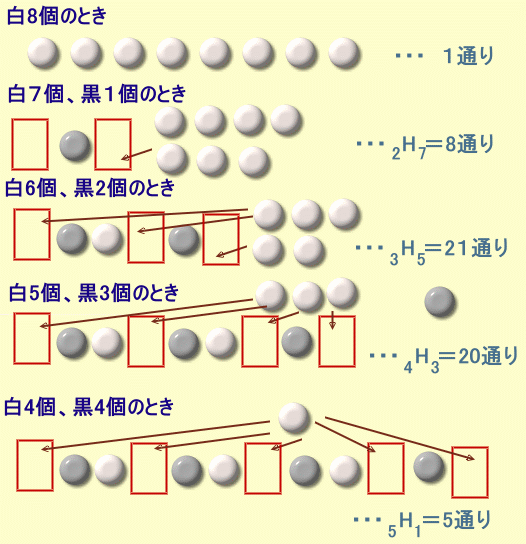
黒石がないとき ・・・ 1通り
黒石が1個のとき
両端の2個所に残りの白石7個を選んで入れること(重複組み合わせ)に相当
・・・ 2H7通り=2+7-1C7通り黒石がn個のとき、(2≦n≦4)
両端および黒石と黒石の間、ただし黒石は隣同士にならないよう、まず白石を間に挟んでおく必要があるので、合計(n+1)個の隙間の中に残りの白石(8−2n−1)個を選んで黒石を入れることに相当 ・・・ nH9-2n通り=9-nC9-2n通り従って、
合計=1+2H7+3H5+4H3+5H1
=1+8C7+7C5+6C3+5C1
=1+ 8+ 21+ 20+ 5
=55通り
となります。
(その他の解法)
- 場合分け、根性 ・・・ とらいしくるさん、ドナルドさん、仮面Xさん、 あほあほまんさん、オリガツさん、土居 千珠さん、小嶋あかりさん、関西一!ロケット・パ〜ンチ (  ̄ー ̄)-○))〜〜〜〜Ю ☆)゜o゜)/ギョさん、 hukuさん、ちっぴ-さん、三国石生さん、きっくさん、ゆっぴさん、 和歌猛さん、ヌオさん、ちひろさん、熱狂的巨人ファンさん、他