第５６問の解答

問題［平面図形]

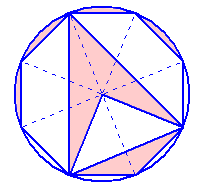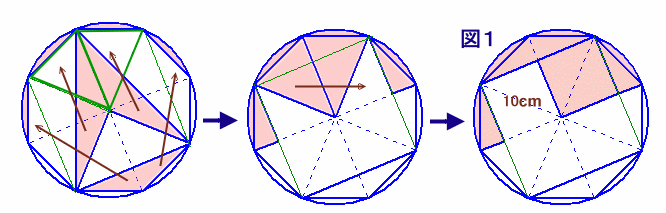
問題図 左図は、半径が１０cmの円と正八角形で出来ています。

赤色の部分の面積は、合計何cm2ありますか。

解答例１［ 半円−直角二等辺三角形］

Banyanyanさん、mhayashiさん、土居　千珠さん、FLONTさん、K.N.I.F.E.さん、 やまけんさん、高橋　道広さん、トシえもんさん、hitoshiさん、TOMOKIさん、 AIRさん、ＪＵＮさん、有無相生さん、仮面Ｘさん、なかさん、 スモークマンさん、ミミズクはくず耳さん、あほあほまんさん、勝浦捨てる造さん、nobuさん、 BEANさん、ショウさん、長野　美光さん、クララさん、とらいしくるさん、 tomhさん、ヌオさん、大岡　敏幸さん、ふじさきたつみさん、ヨッシーさん、 tamahimeさん、ひびき　りょうさん、hukuさん、ゆっぴさん、トトロ＠Ｎさん、 N.Nishiさん、えりぴょんさん、６年のはえぬさん、K.Sさん、（￥￥）さん、 野球＝乱闘党首さん、他

等積変形および移動で考えます。

参考図１

頂角が１３５度の二等辺三角形（大きいほう）は、頂角が４５度の二等辺三角形と等積です。

また、右下の小さいほうの二等辺三角形は２つに分解して移動します。

さらに、斜辺が１０cmの直角二等辺三角形を移動すると、図１のようになります。

従って、
求める面積＝半径１０cmの円×１/２−対角線が１０cnの正方形
　　　　　　　＝３．１４×１０2×１/２−１０2×１/２
　　　　　　　＝（３．１４−１）×１００×１/２
　　　　　　　＝２１４×１/２
　　　　　　　＝１０７cm2
となります。

答　１０７cm2

以上

解答例２［ 図の対称性に注目して赤い部分を整理して解］

２１日ほど前までは、としおとこさん、海夢さん、他

斜めの直径に関して最小だから左半分の面積で考えます。

参考図２　

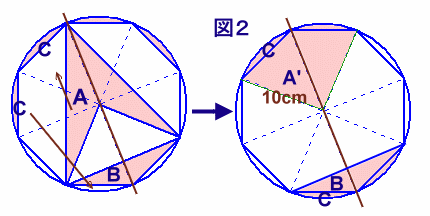
  • A：２辺が１０cmで頂角が１３５度の二等辺三角形

  • B：Aと相似な二等辺三角形の半分

  • C：弓形の部分

  • A'：２辺が１０cmで頂角が４５度の二等辺三角形

とすると、A＝A'だから

  • A'＋C：１/８円

  • B＋C：１/８円−斜辺１０cmの直角二等辺三角形

従って、
求める面積＝（半径１０cmの円×1/８×２−対角線が１０cnの正方形×１/２）×２
　　　　　　　＝３．１４×１０2×１/２−１０2×１/２
　　　　　　　＝１０７cm2
となります。