第５９問の解答

問題［平面図形]

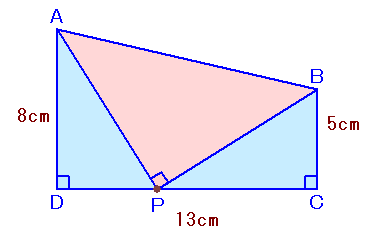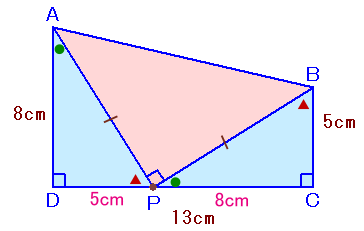
左図のように、∠D＝∠C＝直角の台形ABCDがあります。
また、点Pは台形の辺CD上を自由に移動できる点です。

△ABPが直角二等辺三角形となるような位置にPがあるとき、△ABPの面積は何cm²になりますか？

ただし、辺AD＝８cm、辺BC＝５cm、辺DC＝１３cmです。

解答例１［△ＡＤＰと△ＰＣＢが合同になるように…,台形-直角三角形×２］

C-Dさん、maruhagedonさん、ヌオさん、マッスルさん、ふじさきたつみさん、智美さん、有無相生さん、あああああさん、hukuさん、ねこやんさん、阿仁－汰さん、yumiさん、あほあほまんさん、野球＝乱闘党首さん、abcdeさん、よしけいさん、ＪＵＮさん、evolutionさん、わっさっささん、ざきおさん、由羅さん、　土橋　雅樹さん、やまけんさん、他

∠DAP＋∠APD＝９０°、∠APD＋∠BPC＝９０°、∠BPC＋∠PBC＝９０°より、∠DAP＝∠BPC、∠APD＝∠PBC。
　

従って、△ADPと△PCBは合同となり、
DP＝BC＝５ｃｍ、PC＝AD＝８ｃｍとなります。

よって、
　△APB
＝台形ADCB－（△ADP＋△PBC）
＝１/２×（８＋５）×１３－１/２×５×８×２
＝８４．５－４０
＝４４．５ｃｍ²となります。

答　４４．５cm²

以上

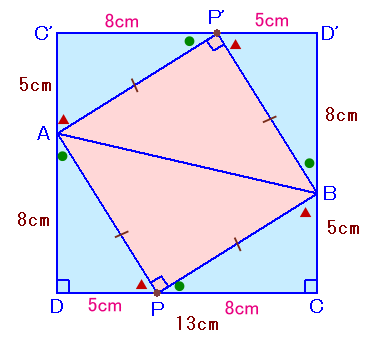
解答例２［相似だと思ったら合同だった、台形２つで正方形、一辺13の正方形］

小杉原啓さん、アキオさん、トトロ＠Ｎさん、ケンタッキー大好き人間さん、ステップ　ばい　ステップさん、とらいしくるさん、　　長野　美光さん、憂鬱さん、みやさん、tekiさん、ゆきおさん、AIRさん、スモークマンさん、ひびき　りょうさん、他

台形を２個合わせて下図のように正方形をつくります。

正方形の一辺＝８＋５＝１３ｃｍ。
△ADP等が２辺が８ｃｍ、５ｃｍの合同な直角三角形であることは、解答例１と同様。

よって、求める面積
＝（１３×１３－１/２×５×８×４）×１/２
＝４４．５ｃｍ²。

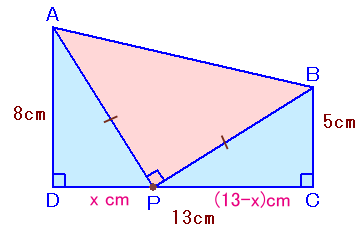
解答例３［三平方の定理、迷わずに三平方、５×１３の長方形を取っ払って三平方］

昨年はとしおとこさん、kasamaさん、阿仁－汰さん、tomhさん、mhayashiさん、トシえもんさん、大岡　敏幸さん、鵬さん、ryoさん、ヨッシーさん、バボちゃんさん、　　辻。さん、N.Nishiさん、じゅうたん島さん、　　大地のパパさん、BEANさん、他

DP＝ｘとします。

　三平方の定理より、
AP²＝８²＋ｘ²、BP²＝（１３－ｘ）²＋５²。
AP＝BPだから、
　８²＋ｘ²＝（１３－ｘ）²＋５²、
　６４＋ｘ²＝１６９－２６ｘ＋ｘ²＋２５
よって、
　ｘ＝（１６９＋２５－６４）×１/２６＝５ｃｍ。
従って、△APB＝１/２×AP²＝１/２×（８²＋５²）＝４４．５ｃｍ²。

（その他の解法）

長方形にしてひいた　・・・　卓球命さん、かみおかさん、他
２元連立方程式　・・・　 koba-shonenさん、他


	台形を２個合わせて下図のように正方形をつくります。正方形の一辺＝８＋５＝１３ｃｍ。 △ADP等が２辺が８ｃｍ、５ｃｍの合同な直角三角形であることは、解答例１と同様。よって、求める面積＝（１３×１３－１/２×５×８×４）×１/２＝４４．５ｃｍ²。