第６０問の解答

問題［規則性]

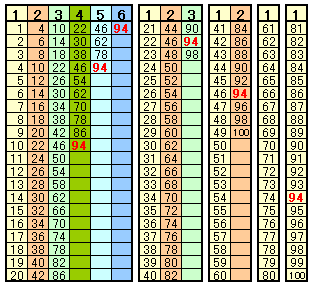
下は、次のきまりにしたがって書き並べられた、100以下の整数の集まりです。

  • 1行目は1を、2行目は2を・・・100行目には100を、最初(左はし)に書く。

  • 各行「もとの整数に1を足してから2倍した数字」を計算して、右に書いていく。

  • 計算された数字が100を超える場合は、書くのをやめる。

1　4　10　22　46　94
2　6　14　30　62
3　8　18　38　78
：
：
：
：
99
100

この集まりの中にでてくる整数の中で、登場する回数が一番多い整数は何ですか？

解答例１［規則性を見つける 、順に書き出した、推理］

トシえもんさん、おかやま産さんさん、OKAYAMAさん、野球＝乱闘党首さん、ショウさん、 マッスルさん、ヌオさん、土居　千珠さん、あさみゆうたさん、午年のうりぼうさん、 ふじさきたつみさん、BEANさん、kasamaさん、tuneさん、仁史さん、 鵬さん、あまれっとさん、 　とらいしくるさん、土居　明弘さん、智美さん、やっぴさん、evolutionさん、 やまけんさん、まるケンさん、ボディスラムさん、歩美サマ×２さん、海夢さん、 キングさん、N.Nishiさん、仮面Ｘさん、他

全て書き出すと下表のようになります。

参考図１

１列目は１ずつ、２列目は２ずつ、３列目は４ずつ、４列目は８ずつ、
５列目は１６ずつ増加し、６列目は９４のみ。

従って、１列に同じ数字は出てこないので、各列とも含まれている９４が、最も個数が多い整数となります。　

答　９４

以上

解答例２［逆算。］

小杉原 啓さん、たかまつ　ろろさん、tomhさん、bumpさん、他

各行の数字について考えてみます。

例えば、第１行では、
　１→４→１０→２２→４６→９４
となっていますが、→の操作は共通なので、
　４→１０→２２→４６→９４
　１０→２２→４６→９４
　２２→４６→９４
　４６→９４
　９４
という行が存在します。

→の操作：１を足して２倍するに対し、逆の操作：２で割り１を引くは一意的なので、ここに出てくる６種類の数字は、上記６行以外には出てきません。

従って、９４は全部で６個出てくることになります。

他の行の長さは５個以下なので、９４以外の数字は５個以下ですので、最も多い数字は９４ということになります。

（その他の解法）