問題[速さの問題]
|
|
|
|
|
|
AからBを通ってCまで行こうとしています。 |
|
|
|
|
|
解答例1[天秤では]
| 高田修成さん、Banyanyanさん、小杉原 啓さん、kasamaさん、たこ焼き@さん、他 |
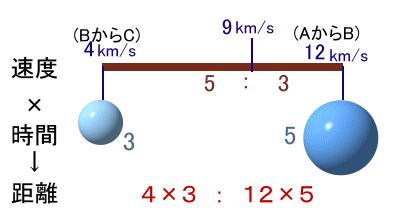
天秤図で考えます。
天秤の目盛りを速度、おもりの重さを時間と考えます。
BからCと平均との目盛り差は9−4=5km/s、
AからBと平均との目盛り差は12−9=3km/s、で5:3。従って、おもりの重さの比は逆比の3:5となります。
よって、距離の比は、4×3:12×3=1:5。
答 5倍
以上
解答例2[面積図より]
| 長野 美光さん、たかし4さん、ねこやんさん、他 |
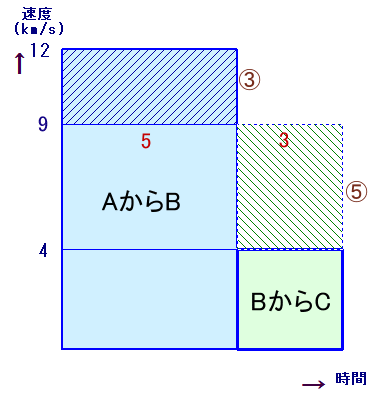
面積図で考えます。
横軸に時間、縦軸に速度をとると、面積が距離となります。
平均速度が9km/sなので、2つの網掛けした長方形の面積は等しくなります。
高さ(速度)の比が(12−9):(9−4)=3:5なので、底辺の長さ(時間)の比は5:3。
従って、距離の比は、12×5:4×3=5:1となりますので、
AからBは、BからCの5倍になります。
(その他の解法)
- 方程式 ・・・ トシえもんさん、野球=乱闘党首さん、N.Nishiさん、evolutionさん、 tani2さん、AIRSさん、hukuさん、午年のうりぼうさん、やまけんさん、 tomhさん、かず。さん、須釜太郎さん、ヒトシさん、mhayashiさん、他
AからBまでの道のりは、BからCまでの道のりのa倍,BからCまでの道のりをxkmとすると、
ax/12+x/4=(a+1)x/9
これを解くと,a=5。