第６４問の解答

問題［割合]

A、B、Cの３人が持っているコインの枚数の比は２：３：４です。
もしAがBから８枚もらい、BがCから何枚かをもらうと、枚数の比は３：４：５になります。
では、Aはコインを何枚持っていますか？

解答例１［比の和を同じにして、総数が同じなので、９と１２の公倍数］

hukuさん、Banyanyanさん、長野　美光さん、高田修成さん、abcdeさん、 航介さん、やまけんさん、☆ひゅお☆さん、tekiさん、ふじさきたつみさん、 けんけんさん、AIRSさん、スモークマンさん、 　あまれっとさん、算数の森さん、勝浦捨てる造さん、たかまつ　ろろさん、C-Dさん、 小杉原 啓さん、たかし4さん、　とらいしくるさん、まるケンさん、ねこやんさん、他

参考図１

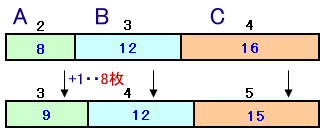
比の和は、それぞれ９と１２なので、公倍数の３６となるようすると、
最初が、８：１２：１６、コインの交換後は９：１２：１５となります。

Ａさんは、９−８＝１だけ増えましたが、これが８枚に相当します。

従って、最初持っていた枚数は、８×８＝６４枚となります。
　

答　６４枚

以上

解答例２［分数にして計算］

ヌオさん、たこ焼き＠さん、小林　真さん、他

参考図２

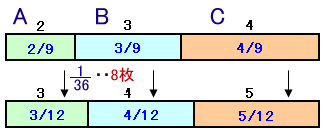
最初にＡさんが持っているのは全体の２/９で、交換後は３/１２なので、
差し引き３/１２−２/９＝１/３６増えたことになり、これが８枚に相当します。

従って、全体の枚数は８×３６＝２８８枚となり、
Ａさんは最初、２８８×２/９＝６４枚持っていたことになります。

（その他の解法）

  • 連立方程式　・・・　 　evolutionさん、土居　千珠さん、野球＝乱闘党首さん、tomhさん、N.Nishiさん、 午年のうりぼうさん、トシえもんさん、かず。さん、mhayashiさん、 ウラールさん、他
    　
  • 普通に方程式　・・・　 　辻。さん、小林　真さん、他
    　
  • 地道に計算　・・・　 　副部長さん、あさみさん、kasamaさん、ヒトシさん、ともあきさん、他