問題[平面図形]
|
|
|
|
|
|
|
 |
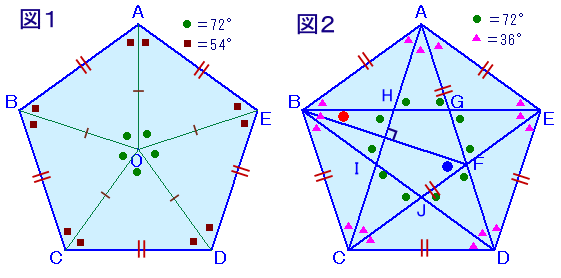
左図でABCDEは正五角形です。 |
|
|
|
|
|
|
解答例1[ひし形と二等辺三角形 、星型対角線のなす角および対称性、見る角度を変えて]
| JUNさん、ともあきさん、とらいしくるさん、junさん、C-Dさん、
kasamaさん、tomhさん、ヒトシさん、あまれっとさん、kobaさん、 N.Nishiさん、ピーターラビットさん、大岡 敏幸さん、三宅彩香さん、 土橋 雅樹さん、他 |
正五角形の中心をOとし、Oと各頂点を結びます。(図1)
また、AC、BDを結んで内部に星形を作り、対称性に着目します。(図2)
図1より、△AOB、△BOC、△COD、△DOE、△EOAは、合同な二等辺三角形で、
頂角=360÷5=72度だから、底角=(180−72)÷2=54度、
従って、正五角形の頂角=54×2=108度と分かります。図2より、△ABE、△BCA、△CBD、△DCE、△EDAは、合同な二等辺三角形で 、
頂角=108度だから、底角=(180−108)÷2=36度、
よって、∠CAD=∠DBE=∠ECA=∠ADB=∠BCD=108−36×2=36度。すると、△AHG、△BIH、△CJI、△DFJ、△EGFは、合同な二等辺三角形で 、
頂角=36度だから、底角=(180−36)÷2=72度となります。よって、△AFE、△CDFなども、底角が72度の合同な二等辺三角形となります。
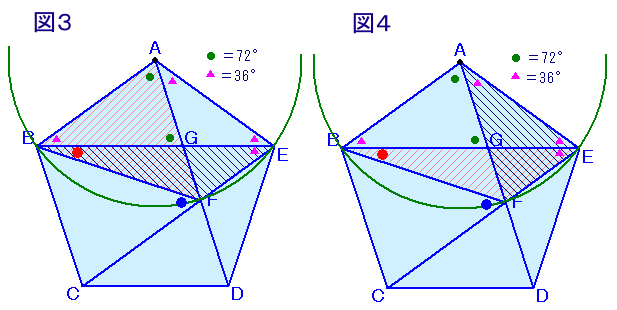
以上から、四角形ABCFは四辺が等しいのでひし形と分かります。
すると、辺BFはひし形の対角線となるので、∠ABC=∠AFC=108度を、それぞれ二等分します。
よって、
∠BFC=∠ABF=108÷2=54度、
∠FBG=∠ABF−∠ABE=54−36=18度
となります。答 54度、18度
以上
解答例2[相似な二等辺三角形から 、bfcをxとして]
| N.Nishiさん、ピーターラビットさん、大岡 敏幸さん、三宅彩香さん、 たこ焼き@さん、他 |
解答例1とほぼ同じですが、図2より、△BFCがCB=CFの二等辺三角形であることが分かります。
よって、
∠BFC=(180−72)÷2=54度と求まります。
以下、同様。
解答例3[円周角と中心角]
| evolutionさん、有無相生さん、他 |
解答例1と同様にして、∠FEB=36度、∠FAB=72度=∠FEB×2が分かります。
従って、図3から、∠FEBはBFに対する円周角、∠FABは中心角となり、
B、F、Eの3点はいずれもAを中心とし、半径をABとする円の周上にある ことが分かります。よって、図4から、∠FBEはFEに対する円周角、∠FAEは中心角となり、
2×∠FBE=∠FAE、
∠FBE=∠FAE÷2=36÷2=18度。また、∠BFCは△BFEの外角だから、
∠BFC=∠FBE+∠FEB=18+36=54度
となります。