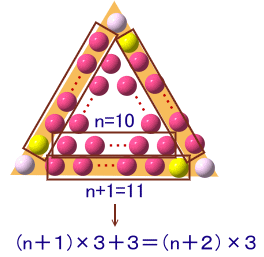第６７問の解答

問題［規則性]

問題図

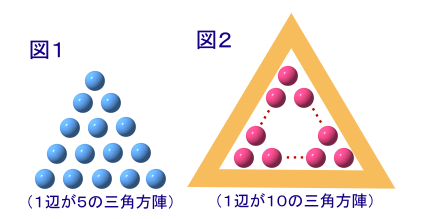左図のように碁石をならべた形を、１辺が５の三角方陣と呼ぶことにします。

同様に１辺が１０の三角方陣をこしらえました。（図２の赤色）

これの周囲（右図の黄色部分）にもう１列づつ碁石を並べるためには、碁石はあと何個必要ですか？

解答例１［1辺の長さを求める、一辺の数、(10+2)×3、（１３−１）×３、(10+3-1)×3］

数学大好きさん、evolutionさん、たこ焼き＠さん、有無相生さん、 ちゃちゃさん、まるケンさん、ちこりんさん、BEANさん、kasamaさん、 tomhさん、るんたったさん、やまけんさん、 　ピーターラビットさん、たかまつ　ろろさん、chi-さん、ブライトさん、bunさん、 bunさん、修平さん、　とらいしくるさん、トシえもんさん、kokiさん、ふじさきたつみさん、長野　美光さん、 　大岡　敏幸さん、野球＝乱闘党首さん、たかし4さん、　DrKさん、他

参考図１

外側の辺の長さは、両端を除けば１０＋１＝１１個、
両端を入れると１０＋３＝１３個となります。

従って、合計では、１１個×３＋３＝３６個必要になります。
（あるいは、（１０＋２）×３＝３６、または（１３−１）×３＝３６と計算することもできます）

答　３６個

以上

解答例２［平行移動、類推 ］

Taroさん、　土居　千珠さん、こえだ§さん、hukuさん、 他

参考図２

中央の赤の部分（１０の三角方陣）を 、左へ１個分、左斜め下に１個分だけ平行移動します。

右側に３列増やすと、新しい三角方陣になりますので、１０＋３＝１３の三角方陣となります。

従って、

  • 右辺の長さは、１３個

  • 下側は、右辺と共通分の１個を除いて１２個

  • 左辺は、右辺と下辺に共通の２個を除いて１１個

合計＝１３＋１２＋１１＝３６個と求まります。

解答例３［実際に・・・・ ］

大吉さん、他

参考図３

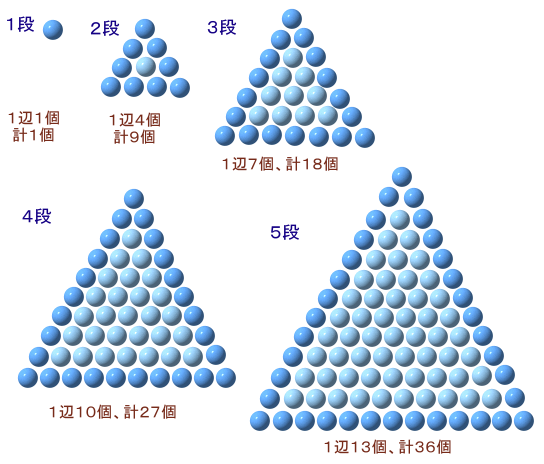
実際に碁石を並べてみます。

２の三角方陣の次が５の三角方陣なので、辺の長さは、周囲を１段増やす毎に３個ずつ増えていきそうです。

そこで、１の三角方陣から出発して１段ずつ増やしていくと、
　１→４→７→１０→１３
となり、１０の三角方陣の次は１３の三角方陣で、周囲に３６個が必要なことが分かります。