問題[平面図形]
|
|
|
|
|
|
|
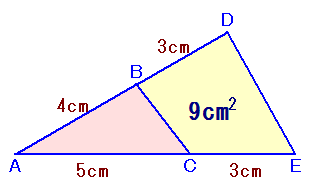 |
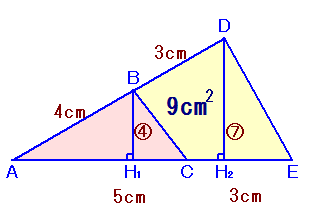
左図の四角形BCEDは、面積=9cm2は、AB=4cm、BD=3cm、AC=5cm、CE=3cmです。 では、△ABCの面積は何cm2になりますか? |
|
|
|
|
|
|
解答例1[角を同じくする三角形の面積の比はその角を はさむ辺の積に比例、 BとDからAEに垂線を下ろす]
| 土居 千珠さん、野球=乱闘党首さん、修平さん、damotoさん、hukuさん、 こえだ§さん、あまれっとさん、トシえもんさん、信三さん、 まるケンさん、やまけんさん、kasamaさん、evolutionさん、るんたったさん、 スモークマンさん、AIRSさん、 seigiさん、他 |
BおよびDから辺AEに下ろした垂線の足をH1、H2とします。
△ABH1と△ADH2は相似だから、BH1:DH2=BA:DA。
従って、
△ABC:△ADE
=1/2×AC×BH1:1/2×AE×DH2
=AC×BA:AE×DA
=5×4:8×7
=5:14。よって、
△ABC:四角形BCDE=5:9従って、
△ABC=四角形BCDE×5/9=5cm2
となります。答 5cm2
以上
解答例2[DからCに補助線を引いて三角形の面積比を]
| ペンギンさん、ちこりんさん、tomhさん、ぶさん、ぺんこさん、 なるみさん、ぶぁさん、Mr.Knightさん、他 |
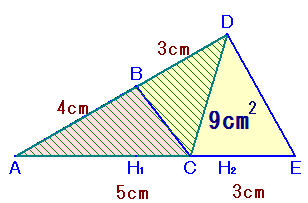
DとCを結びます。
高さが等しい三角形の面積は、底辺の比に等しいので、
△ADC:△ADE=AC:AE ・・・ (1)
△ABC:△ADC=AB:AD ・・・ (2)。(1)×(2)より、
△ADC×△ABC:△ADE×△ADC=AC×AB:AE×ADよって、
△ABC:△ADE=AC×AB:AE×AD=5×4:8×7以下、解答例1と同様。
(その他の解法)
- △DBCの高さをX、△DCEの高さをYとして方程式を解く ・・・ 大地のパパさん、shuさん、 他