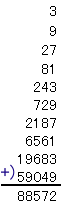第６９問の解答

問題［規則性]

次の式を計算してください。

3＋9＋27＋81＋243＋・・・・・・＋59049

解答例１［(59049*3-1)÷2-1、59049を素因数分解して、前の数までの和の算出]

まるケンさん、Ｍｒ.Ｋｎｉｇｈｔさん、鳳仙花さん、有無相生さん、 kasamaさん、tomhさん、ふじさきたつみさん、tekiさん、ryoさん、
寺脇犬さん、午年のうりぼうさん、かすみんさん、　松本　時博さん、成立　飛鳥さん、他

９＝３×３、２７＝９×３、８１＝９×３、２４３＝８１×３、・・・、
となっているので、各項は、それぞれ前の項の３倍になっています。
（等比数列：一般式＝３^k）

求める合計をS（上記、式（１））とおき、S×３（上記、式（２））を計算してみます。
式（２）を一つずらすと第２～１０項までが等しくなることが分かります。

従って、（２）－（１）より、
　S×２＝１７７１４７－３＝１７７１４４
よって、S=１７７１４４÷２＝８８５７２と求まります。

答　８８５７２

以上

解答例２［３+３の二乗+３の３乗+・・・+３の１０乗、等比数列の和の公式］

とらいしくるさん、N.Nishiさん、遠藤平吉さん、大岡　敏幸さん、　かず。さん、他

（参考）等比数列の和の公式の求め方

初項a、公比rの等比数列の一般項はa×r^k-1と表せます。

第n項までの和をSとすると、　
　　S＝a＋a×r＋a×r²＋a×r³＋・・・＋a×r^n-1　　　　　　・・・（１）
S×r＝　　a×r＋a×r²＋a×r³＋・・・＋a×r^n-1＋a×rⁿ　・・・（２）

（２）－（１）より、
　S×(r-1)＝a×rⁿ－a＝a×（rⁿ－１）

よって、
　S＝a×（rⁿ－１）／(r-1)
と求まります。

3＋9＋27＋81＋243＋・・・・・・＋59049は、
初項３、公比３の等比数列の第１０項までの和となります。

従って、上記公式を適用すれば、
　和＝３×（３¹⁰－１）／（３－１）
　　＝３×（５９０４９－１）／２
　　＝（１７７１４７－３）／２
　　＝８８５７２
と求まります。

解答例３［そのまま計算する、紙に書いて計算する、かける3］

ぺんこさん、Taroさん、るんたったさん、ぶぁさん、evolutionさん、野球＝乱闘党首さん、ＪＵＮさん、AYAKAさん、野球＝乱闘党首さん、hitoshiさん、 tataさん、shioriさん、　shioriさん、shioriさん、　ピーターラビットさん、他

3＋9＋27＋81＋243＋・・・・・・＋59049が、公比３の等比数列の和であることに気づけば、
紙に書くなどして直接計算することができます。

（その他の解法）

(1+3の5乗）（3+3の2乗+・・+3の5乗）　・・・　土居　千珠さん、こえだ§さん、他

　

　

　

　


	９＝３×３、２７＝９×３、８１＝９×３、２４３＝８１×３、・・・、となっているので、各項は、それぞれ前の項の３倍になっています。（等比数列：一般式＝３^k）求める合計をS（上記、式（１））とおき、S×３（上記、式（２））を計算してみます。式（２）を一つずらすと第２～１０項までが等しくなることが分かります。従って、（２）－（１）より、　S×２＝１７７１４７－３＝１７７１４４よって、S=１７７１４４÷２＝８８５７２と求まります。答　８８５７２以上


	3＋9＋27＋81＋243＋・・・・・・＋59049が、公比３の等比数列の和であることに気づけば、紙に書くなどして直接計算することができます。