第７０問の解答

問題［場合の数]

1から100までの整数の中に、
　「３か７のいずれかの数字を使っていて、４と９のどちらの数字も使っていない」
ような整数は何個ありますか？

解答例１［数えました 、表！、]

あまれっとさん、こえだ§さん、ぶぁさん、土居　千珠さん、嘉門　徹さん、トシえもんさん、ピーターラビットさん、たこ焼き＠さん、ＳＡＲＡさん、hukuさん、 浩史さん、MrYutaさん、Taroさん、鎌倉時代さん、akisatoさん、土橋　雅樹さん、tyomiyaさん、ハッセ　パセリさん、evolutionさん、kunioさん、 るんたったさん、kasamaさん、ヌオさん、tomhさん、N.Nishiさん、やまけんさん、ふじさきたつみさん、なるみさん、ともひろさん、あだださん、3.141592さん、他

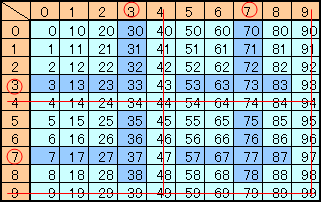
表に書いて数えてみます。

参考図１

  • １０の位が３、４、７、９以外のとき　・・・　１の位が３または７の２個

  • １０の位が３または７のとき　・・・　１の位が４および９以外の８個

  • １０の位が４または９のとき　・・・　不適

従って、
　合計＝（１０−４）×２＋２×（１０−２）
　　　　＝２８個
と求まります。

答　２８個

以上

解答例２［（10-4）×2＋（10-2）×2、10×2＋（10-2）×2−4×2、40-4-8］

とらいしくるさん、大岡　敏幸さん、ryoさん、yukiさん、野球＝乱闘党首さん、Happyさん、abcdeさん、Ｍｒ.Ｋｎｉｇｈｔさん、他

若干考え方が異なりますが、同じ分類にしてみました。
解答例１の表を参照しながら確認するといいでしょう。

解答例３［2×8×2-4］

長野　美光さん、ちこりんさん、辻。さん、まるケンさん、他

参考図２

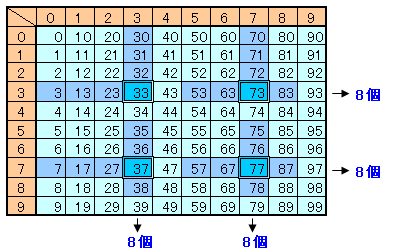
  • １０の位が３または７で、１の位が４でも９でもない数　：　２×８個　・・・（１）

  • １の位が３または７で、１０の位が４でも９でもない数　：　２×８個　・・・（２）

  • １０の位、１の位とも３または７　：　２×２個　・・・　（３）

求める個数＝（１）＋（２）−（３）＝１６＋１６−４＝２８個

解答例４［８×８−６×６[変則ｎ進法]］

C-Dさん、他

参考図３

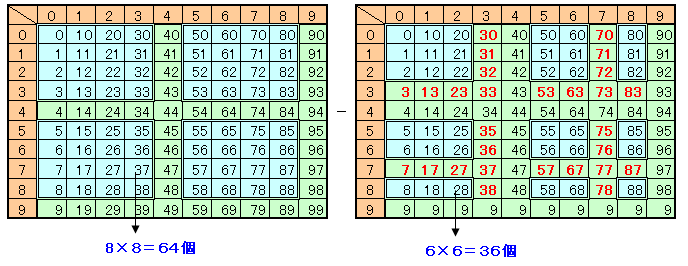
  • 数字に４および９を含まない数　：　８×８＝６４個　・・・　（１）

  • 数字に４、９、３、７を含まない数　：　６×６＝３６個　・・・　（２）

求める個数＝（１）−（２）＝６４−３６＝２８個