第７２問の解答

問題［整数の性質]

２つの整数があって、大きさの比は３：１１です。
この２数の最小公倍数が１０８９のとき、小さい方の整数はいくつですか？

解答例１［２数を 3a,11a とおいてみる]

mhayashiさん、ふじさきたつみさん、あまれっとさん、あほあほまんさん、土居さん、97年度TORAの門下生(当時14歳)さん、長野　美光さん、Taroさん、tomhさん、 ψ(プサイ)さん、野球＝乱闘党首さん、Ｍｒ.Ｋｎｉｇｈｔさん、躍る大捜査線さん、ちこりんさん、 hitoshiさん、evolutionさん、他

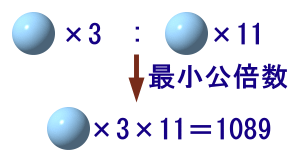
２つの整数は、最大公約数を●で表すと、●×３と●×１１になります。

３と１１は互いに素だから、２つの整数の最小公倍数は●×３×１１＝１０８９。

よって、小さい方の整数＝●×３＝１０８９÷１１＝９９と求まります。

答　９９

以上

解答例２［素因数分解]

とらいしくるさん、ぺんこさん、寺脇犬さん、三宅彩香さん、午年のうりぼうさん、大岡　敏幸さん、kasamaさん、みかんさん、やまけんさん、たみんごさん、他

１０８９＝３²×１１²と素因数分解できます。

２つの整数の比＝３：１１なので、これらは
　３²×１１と３×１１²と
なります。

従って、小さい方の整数＝３²×１１＝９９と求まります。

（その他の解法）

比に実数をかける　・・・　るーちゃんさん、嘉門　徹さん、土橋　雅樹さん、他


	２つの整数があって、大きさの比は３：１１です。この２数の最小公倍数が１０８９のとき、小さい方の整数はいくつですか？


	１０８９＝３²×１１²と素因数分解できます。２つの整数の比＝３：１１なので、これらは　３²×１１と３×１１²となります。従って、小さい方の整数＝３²×１１＝９９と求まります。