問題[平面図形]
|
|
|
|
|
|
|
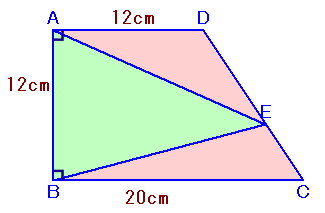 |
左図は、∠A=∠B=直角になっている台形ABCDを、点Eをもとに3か所に分けたものです。 △ADEと△BCEの面積が等しいとき、△ABEの面積は何cm2になりますか? |
|
|
|
|
|
|
解答例1[ 赤い部分の高さの比が5:3]
| ヌオさん、mhayashiさん、とらいしくるさん、松本 時博さん、あまれっとさん、 ぺんこさん、信三さん、たみんごさん、ふじさきたつみさん、鎌倉時代さん、 長野 美光さん、hukuさん、大岡 敏幸さん、hitoshiさん、evolutionさん、 masaさん、辻。さん、shuさん、C-Dさん、kasamaさん、 tomhさん、tekiさん、nakamotoさん、智乃介さん、lkさん、 アラちゃんさん、keijiさん、5年生の父さん、キングさん、 JUNさん、ちこりんさん、ペンギンさん、他 |
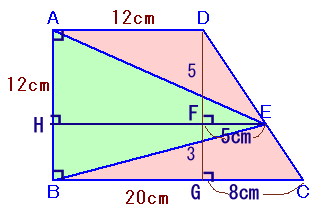
EからABに下ろした垂線の足をそれぞれHとし、DからHE、BCに下ろした垂線の足をF、Gとします。
△ADE=1/2×AD×DF、△BCE=1/2×BC×FG。
△ADE=△BCEより、DF:FG=BC:AD=5:3。
AD=HF=BG=12cm、よってGC=20−12=8cm。
△DFEと△DGCは相似で、相似比は5:3、
よって、FE=GC×3/8=5cm。従って、HE=HF+FE=12+5=7cm。
よって、△ABE=1/2×AB×HE=1/2×12×17=102cm2と求まります。
答 102cm2
以上
(その他の解法)
- ADEの高さをxとして△ADEと△BCEの式をつくり解く ・・・ ψ(プサイ)さん、nakamotoさん、かず。さん、5年生の父さん、辻さん、たこ焼き@さん、 他
- 方眼紙を用いて正確に図を書きます眼を数える ・・・ 中島さん、長谷川 徹さん、 他