問題[規則性]
|
|
|
|
|
|
掛ける数、または掛けられる数のどちらかに9のつく九九は17個あります。 この17個全部の答の和はいくらありますか? |
|
|
|
|
|
解答例1[9×(1+2+…+9)×2-9×9、{2×(1+2+3+4+5+6+7+8)+9}×9、{(9+72)+(18+63)+(27+54)+(36+45)}×2+81]
| みかんさん、野球=乱闘党首さん、ラムウさん、辻さん、 鎌倉時代さん、まるケンさん、あまれっとさん、hukuさん、ふじさきたつみさん、 土橋 雅樹さん、kasamaさん、大岡 敏幸さん、tomhさん、エガオヲミセテさん、 MrYutaさん、AYAKAさん、 ヌオさん、智乃介さん、長野 美光さん、午年のうりぼうさん、たみんごさん、 shuさん、辻。さん、たかし4さん、lkさん、かず。さん、 とらいしくるさん、 翔太さん、たこ焼き@さん、5年生の父さん、evolutionさん、嘉門 徹さん、 他 |
九九の表を下記に示します。
すると、
掛けられる数が9:
1×9+2×9+・・・+9×9=(1+2+・・・+9)×9 ・・・ (1)掛けられる数が9:
9×1+9×2+・・・+9×9=9×(1+2+・・・+9) ・・・ (2)掛ける数も掛けられる数も9:
9×9 ・・・ (3)(3)が(1)、(2)の両方に含まれるので、
求める和=(1)+(2)−(3)
=(1+2+・・・+9)×9+9×(1+2+・・・+9)−9×9
=45×9+9×45−9×9
=(45+45−9)×9
=81×9
=729
と、求まります。答 729
以上
解答例2[3乗数になるから 、シグマ・等差数列]
| ぶぁさん、Taroさん、前田智史さん、にゃンタさん、ボディスラムさん、ryoさん、 他 |
解答例1と同様にして、
求める和=(1)+(2)−(3)
=(1+2+・・・+8)×9+9×(1+2+・・・+8)+9×9
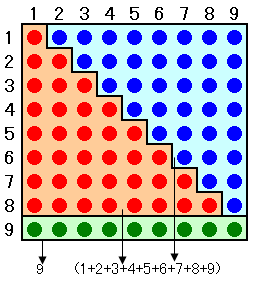
={(1+2+・・・+8)+(1+2+・・・+8)+9}×9
と表せます。
すると上図より、
(1+2+・・・+8)+(1+2+・・・+8)+9=9×9
が分かるります。従って、
求める和=9×9×9=729
と求まります。
(その他の解法)
- 紙に書いて計算する。 ・・・ shioriさん、hitoshiさん、ぺんこさん、がいさん、他
- Excelで計算する。 ・・・ 小田嶋さん、 他