問題[規則性]
|
|
|
|
|
|
1、2、3、5、7、9、10、・・・ |
|
|
|
|
|
解答例1[逆に4または6で割り切れる個数を求める 、2004として計算、ベン図]
| mhayashiさん、あまれっとさん、shiaroさん、辻さん、ゆうしゃさん、沙月さん、MrYutaさん、ふじさきたつみさん、有無相生さん、hitoshiさん、寺脇犬さん、ぺんこさん、shuさん、C-Dさん、kasamaさん、のりてけさん、たみんごさん、かず。さん、るんたったさん、seigiさん、しょうちゃんさん、ψ(プサイ)さん、ヌオさん、小林 真さん、長野 美光さん、パーポンさん、 大岡 敏幸さん、 ペンギンさん、他 |
4または6で割り切れる整数の個数を求めることにします。
4で割り切れる整数=4の倍数:
2003÷4=500.75 → 500個 ・・・ (1)6で割り切れる整数=6の倍数:
2003÷6=333.83... → 333個 ・・・ (2)4および6で割り切れる整数=12(4と6の最小公倍数)の倍数:
2003÷12=166.91... → 166個 ・・・ (3)従って、
4または6で割り切れる整数=(1)+(2)−(3)=500+333−166=667個よって、4でも6でも割り切れない整数=2003−667=1336個となり、
2003は1336番目に出てくることが分かります。答 1336番目
以上
解答例2[4と6の公倍数12を一周期]
| みかんさん、ゆうしゃさん、ryoさん、Taroさん、前田智史さん、 辻。さん、まるケンさん、5年生の父さん、tomhさん、エガオヲミセテさん、 ちゅんこの姉さん、ゆううつさん、他 |
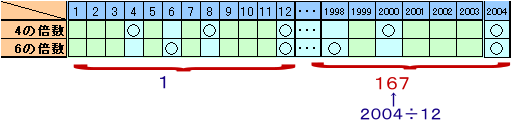
4と6の最小公倍数12を周期として考えます。
1から12までの間で、4でも6でも割り切れない数は、
1、2、3、5、7、9、10、11
の8個あります。2004÷12=167なので、1から2003まででは、
8×167=1336個
あることが分かります。