第７７問の解答

問題［推理 （虫食い算）]

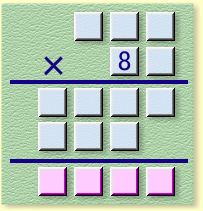問題図 左図の式の□に１つずつ数字を入れて、式を完成させて下さい。

完成させたら、この掛け算の答えとなる４ケタの整数を答えて下さい。

解答例１［順番に□を決めていく ]

mhayashiさん、沙月さん、あまれっとさん、有無相生さん、ＮＥＵＴＲＡＬさん、 辻さん、ψ（プサイ）さん、トシえもんさん、Yyukomamaさん、りかさん、 ピーターラビットさん、tomhさん、shiaroさん、前田智史さん、hukuさん、 Ｋｎｉｇｈｔさん、damotoさん、他

参考図１

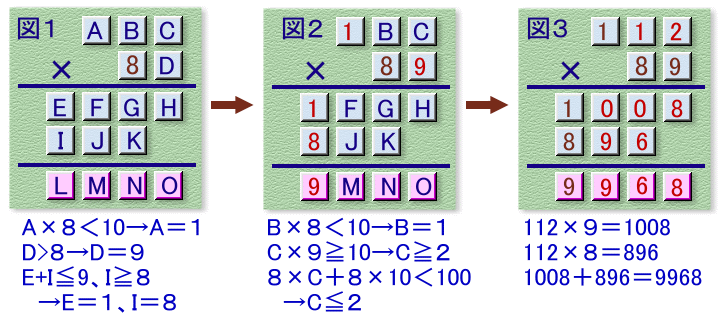
図１のように各数字に記号をつけます。

ＡＢＣ×８＝ＩＪＫと、掛け算の結果が３ケタとなることから、Ａ＝１が決まります。

また、Ｅ＋Ｉが繰り上がらないので、９以下。
ところが、Eは１以上で、Iは１×８＝８または１×８＋１＝９。
従って、E＝１、I＝８と決まります。

次に、１BC×８が３ケタ、１BC×Dが４ケタとなることから、D＞８、
すなわち、D＝９が求まります。

また、Ｂ×８が繰り上がらないことより、Ｂ＝１となります。

１１C×９が４ケタの数より、C≧２、
１１Ｃ×８＝３ケタの数より、Ｃ≦２、
よって、C=２と決まります。

よって、本問の掛け算は、１１２×８９＝９９６８と決まります。

答　９９６８

以上

解答例２［範囲を少しずつ絞る 、89をかけて9999未満の数、９９９９÷８９、最上段の数として8をかけて900未満に]

みかんさん、ゆうしゃさん、S@TORUさん、たみんごさん、マッスルさん、大岡　敏幸さん、藤原舞さん、かず。さん、koba-shonenさん、lkさん、るんたったさん、とらいしくるさん、寺脇犬さん、ふじさきたつみさん、長野　美光さん、信三さん、しょうちゃんさん、鳳　奥人さん、ジルドさん、 他

参考図２

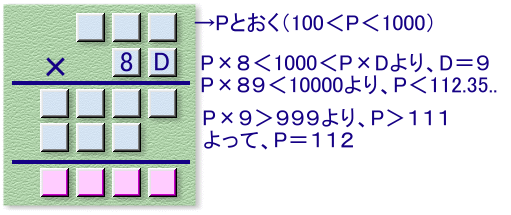
掛けられる数をP、掛ける数を８Dとおきます。

Pに８を掛けて３ケタ、Dを掛けて４ケタとなることから、Dは８より大きい。
よって、D＝９と決まります。

Pに８９を掛けて４ケタの数となることから、P×８９＜１００００。
P＜１００００÷８９＝１１２．３５...　・・・　（１）.

また、Pに９を掛けて４ケタの数となることから、P×９＞９９９。
P＞９９９÷９＝１１１　・・・　（２）

（１）、（２）より、P＝１１２と決まります。

よって、掛け算の結果は、１１２×８９＝９９６８。

（その他の解法）

  • プログラムを書く　・・・　ハラギャーテイさん、kasamaさん 他