問題[平面図形]
|
|
|
|
|
|
|
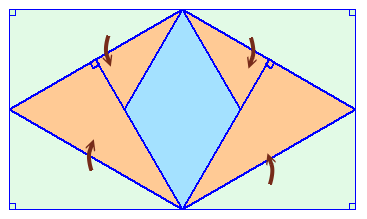 |
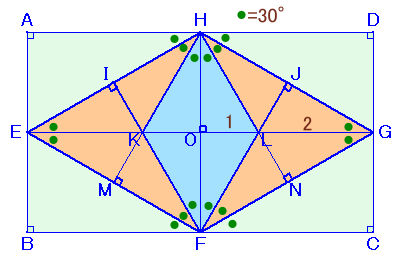
表が青色で裏が黄色の長方形の形をした紙があります。 もとの長方形の面積が240cm2のとき、見えている青色部分の面積は何cm2になりますか? |
|
|
|
|
|
|
解答例1[小さな三角形は大きな三角形の三分の一 、比を使う、24分割のうちの4個分、ひし形を対角線で分けて、正三角形の法則利用、同じ大きさを見つける]
| とらいしくるさん、yukiさん、栗原さん、長野 美光さん、算数大好きさん、 tomhさん、戸村秀志さん、MOICHIさん、沙月さん、ゆうしゃさん、 川村 高雅さん、Taroさん、caniさん、有無相生さん、lasalleさん、 C-Dさん、宮前春美さん、えいみさん、elmotitiさん、kasamaさん、 hukuさん、算数大好きさん、仮面Xさん、大岡 敏幸さん、Gotchanさん、shiaroさん、藤田知未さん、藤原舞さん、他 |
下図のように各点に名前を付けて考えます。
△FGJは△FGCの折り返しだから、∠GFC=∠GFJ、∠GJG=∠C=90度、
対称性より、∠HGO=∠FGO、平行線の錯角より、∠FGO=∠GFC。よって、∠GFJ=∠FGO=∠HGOとなりますが、
これらの合計は、180度−∠FJG=90度だから、それぞれは30度。従って、△GHFはGH=GFの二等辺三角形で頂角HGF=60度だから、正三角形となります。また、Lは正三角形△GHFの垂心(重心)だから、GL:LO=2:1。
よって、 △HOL=△HOG×1/3。
同様に、△HOK=△HOE×1/3、△FOL=△FOG×1/3、△FOK=△FOE×1/3。従って、
菱形HKFM=菱形HEFG×1/3
=長方形ABCD×1/2×1/3
=240×1/6
=40cm2
と求まります。答 40cm2
以上