第８１問の解答

問題［場合の数]

６個のみかんを、A、B、Cの３人に 余りなく配ります。
各自に少なくとも１個は配るものとすると、みかんの配り方は何通り考えられますか？

解答例１［組み合わせを使う]

Gotchanさん、あまれっとさん、ちこりんさん、午年のうりぼうさん、C-Dさん、 栗原さん、ペンギンさん、mhayashiさん、ふじさきたつみさん、kasamaさん、 tomhさん、寺脇犬さん、Taroさん、長野　美光さん、かずみさん、 サラのパパさん、Yyukomamaさん、ψ(プサイ)さん、他

各自に配られた個数より１個を除いて考えることにします。
すると、３個のみかんをA、B、Cに重複を許して配る重複組み合わせの問題になります。

従って、配り方は
　3H3＝3+3-1C3＝５!/3!2!＝１０通り
と求まります。

これは下図のように考えると分かりやすいでしょう。

参考図１

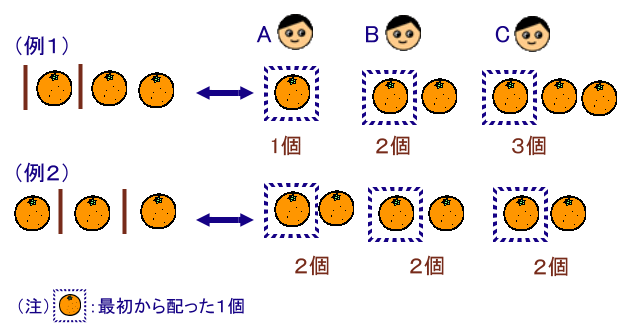
５個の箱に、みかん（●）３個と仕切り（｜）２個を 入れると考えます。
仕切りにはさまれたみかん＋１個をそれぞれA、B、Cに配ることにすると、　・・・（１）
重複組み合わせの配り方と１：１に対応していることが分かります。

例えば、
　例１では、｜●｜●●⇔A：１＋０＝１個、B：１＋１＝２個、C：１＋２＝３個
　例２では、●｜●｜●⇔A：１＋１＝２個、B：１＋１＝２個、C：１＋１＝２個
のように対応します。

（１）の配り方は、５個の箱から３個選んでみかんを入れ、残りの箱には仕切りを入れる
ことにすると、5C3＝１０通りと求まります。

一般には、n個のものをm人に重複して配る場合は、仕切りの個数＝n＋m-１として、
　　nHm＝n+m-1Cn
となります。

答　１０通り

以上

解答例２［場合わけ、順列で求める 、Cでやる、俺はこうして解いた・・・:]

川村　高雅さん、とらいしくるさん、へさん、有無相生さん、西村　辰夫さん、 　 藤原舞さん、沙月さん、西村　辰夫さん、 　あきあきさん、かず。さん、 　谷口　英之さん、他

解答例１と同様に、１個を除いた個数で考えます。

参考図２

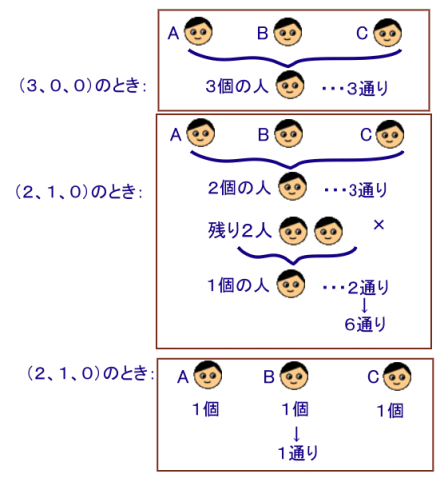
配り方のパターンは、（３、０、０）、（２、１、０）、（１、１、１）の３通りになります。

  • （３、０、０）のとき：
    ３個配る人を３人の中から１人選ぶ→3C1＝３通り
    　

  • （２、１、０）のとき：
    ２個配る人を３人の中から１人選び、１個配る人を残り２人から１人選ぶ
    　→3C1×2C1＝６通り
    　

  • （１、１、１）のとき：１通り

従って、合計＝３＋６＋１＝１０通りとなります。

解答例３［地道に数える]

Gotchanさん、こえだ§さん、ふうきさん、AYAKAさん、土橋　雅樹さん、 Ｋｎｉｇｈｔさん、kuroppyさん、ぶぁさん、yukiさん、lasalleさん、 るんたったさん、ぺんこさん、ミナさん、まっぽさん、西村　辰夫さん、 古市　大剛さん、shiaroさん、他

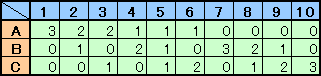
今回も１個を除いた個数で考えます。

参考図３

Aの個数、Bの個数、Cの個数をそれぞれ多い順に数え上げると、上記のようになりますので、
全部で１０通りと求まります。