第８２問の解答

問題［推理]

A，B，C，D，E，Fの６チームが各対戦相手と１回ずつ対戦する総当たり戦があります。
Aはすでに他の５チームとの対戦を全て終え、Bは４チームとの対戦を終えています。
また、Cは３チームと、Dは２チームと、Eは１チームとの対戦を終えています。
このときFは何チームとの対戦を終えていますか？

解答例１［対戦表を作る、消去法、 対戦総数は常に偶数、六角形の辺と対角線]

mhayashiさん、ふうきさん、土居　千珠さん、あまれっとさん、土橋　雅樹さん、 藤原舞さん、マッスルさん、伸樹さん、寺脇犬さん、とらいしくるさん、 辻さん、エニグマさん、智乃介さん、Taroさん、りかさん、 まるケンさん、ジャックさん、elmotitiさん、kasamaさん、三浦晃祐さん、 ぺんこさん、tomhさん、呑さん、Ｋｎｉｇｈｔさん、午年のうりぼうさん、 かず。さん、沙月さん、大吉さん、hitoshiさん、ふじさきたつみさん、 yukiさん、J. M. Cornさん、Yyukomamaさん、大岡　敏幸さん、サラのパパさん、 ψ(プサイ)さん、宏樹さん、ティーハラさん、すうさん、日付変更人さん、 hukuさん、　あきあきさん、C-Dさん、たかし4さん、他

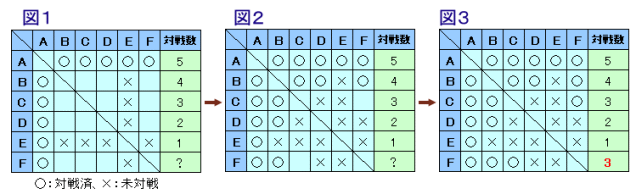
下図のような対戦表で考えることにします。
参考図１

まず、Aは全てのチームと対戦済みなので、EもAと対戦していることが分かります。
ところが、Eの対戦数は１なので、A以外のB、C、D、Fとは未対戦となります。　・・・　図１

次に、Bについて考えると、Bは対戦数４だから未対戦は１試合となります。
上記からBはEと未対戦と分かっているので、残りのC、D、Fとは対戦済みと分かります。
従って、DはA、Bともに対戦済みとなりますが、対戦数２なので残りのC、E、Fとは未対戦となります。　・・・　図２

すると、CはA、Bと対戦済み、D、Eとは未対戦となりますが、対戦数は３なので残ったFとは対戦済みと分かります。　・・・　図３

以上から、全ての対戦状況が分かりました。
FはA、B、Cと対戦済み、D、Eと未対戦となり、対戦数は３と分かります。

答　３試合

以上

（その他の解法）

  • Scherrerの定理？？の利用　・・・　 大野雄平さん、 他