問題[平面図形(軌跡)]
|
|
|
|
|
|
|
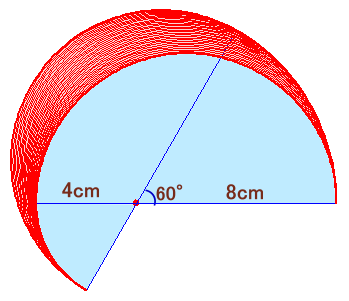 |
直径が12cmの半円を、左図のように直径の端から4cmのところにある点(●)を中心に、60度回転させました。 このとき半円の弧が通過した部分(網線部分)の面積は何cm2になりますか? |
|
|
|
|
|
|
解答例1[全体から白を引く 、計算、相似形らしきもの]
| Gotchanさん、masaさん、あまれっとさん、shiaroさん、taonさん、 午年のうりぼうさん、MrYutaさん、ぺんこさん、C-Dさん、 沙月さん、Taroさん、まるケンさん、川村朗さん、kasamaさん、 ちずさん、Yyukomamaさん 、 まことさん、 たかのりさん、 他 |
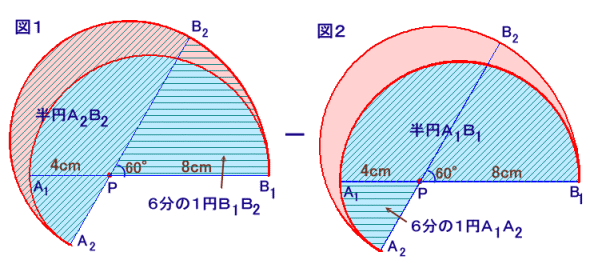
半円A1B1が60度だけ反時計回りに回転し、半円A2B2になったものとします。
(軌跡のアニメGIF)
求める面積をSとすると、
S=(半円A2B2+六分の1円A1A2)−(半円A1B1+六分の1円B1B2)
と表せます。半円A2B2と半円A1B1は、合同だから面積は等しいので、
S=六分の1円A1A2−六分の1円B1B2
=1/6×3.14×82−1/6×3.14×42
=1/6×(64−16)×3.14
=8×3.14
=25.12cm2
と求まります。(参考)等積変形するアニメGIF(長野 美光さんによる )
答 25.12cm2
以上