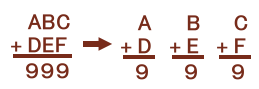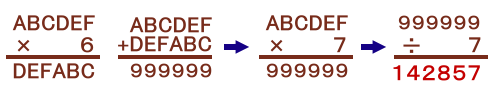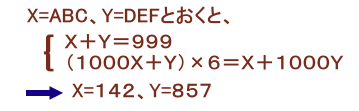問題[整数の性質(虫食い算)]
|
|
|
|
|
|
6個の異なる数字を並べて、ABCDEFという6ケタの整数を作ります。 この整数ABCDEFは何ですか? |
|
|
|
|
|
解答例1[普通に当てはめる 、A+D=B+E=C+F=9、筆算にして当てはめる、もみほぐす:]
| ふうきさん、光希魔宇数(ミッキーマウス?)さん、デンガミジョーさん、吉田佳薫さん、shiaroさん、 大岡 敏幸さん、智乃介さん、とらいしくるさん、みかんさん、ぺんこさん、 浜直君さん、snowさん、アラちゃんさん、kasamaさん、HAJIさん、 塾教師さん、パリンさん、沙月さん、戸村秀志さん、 Knightさん、TOMMYさん、算数人間さん、ショウさん、パァ〜子さん、 Yyukomamaさん、 智乃介さん、理一さん、 ライスさん、他 |
虫食い算で考えてみましょう。まず、A+D=1、B+E=1、C+F=1を示します。
1桁の整数2個の和は18以下なので、C+Fの下1桁が9より、C+F=1となります。
C+Fの桁上がりがないことから、B+Eの下1桁が9となり、同様にしてB+E=1となります。
B+Eの桁上がりがないことから、A+Dの下1桁が9となり、同様にしてA+D=1となります。
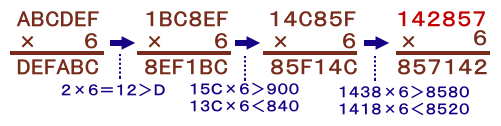
まず、A≧2ならA×6>10と桁上がりするので、A=1、よって、D=9−A=8となります。
次に、B≧5なら、15C×6>150×6=900となり不適、
また、B≦3なら、13C×6<140×6=840となり不適、
よって、B=4、E=9−B=5となります。次に、C≧3なら、F≦5となるが、1438×6>1430×6=8580となり不適、
また、C=1なら、F=8となるが、1418×6<1420×6=8520となり不適、
よって、C=2、F=9−C=7となります。よって、ABCDEF=142857と求まります。
答 142857
以上
解答例2[999999÷7、1/7が142857]
| TORAさん、あまれっとさん、ちこりんさん、長野 美光さん、寺脇犬さん、 あきあきさん、C-Dさん、kunioさん、まるケンさん、ふじさきたつみさん、 他 |
A+C=B+E=C+F=1より、ABCDEF+DEFABC= 999999となります。
ところが、DEFABC=ABCDEF×6なので、
ABCDEF+DEFABC=ABCDEF×(1+6)=999999よって、
ABCDEF=999999÷7=142857
と求まります。(別解)1/7=0.142857...の循環小数になります。
X=0.ABCDEF...のような循環小数を考えます。
6X=0.DEFABC...なので、これらを加えると、
7X=0.999999...=1よって、X=1/7=0.142857...
ABCDEF=142857
と求まります。
解答例3[連立方程式]
| ちずさん、有無相生さん、tomhさん、みゆきさん、 N.Nishiさん、他 |
X=ABC、Y=DEFとおきます。
題意より、
X+Y=999 ・・・ (1)
および
(1000X+Y)×6=X+1000Y
5999X=994Y
857X=142Y ・・・ (2)(1)×142より、
142X+142Y=142X+857X=999X=999×142
よって、X=142、Y=857を得ます。従って、ABCDEF=142857と求まります。
(別解)
(2)より、857は素数なので142と互いに素、
よって、Xは142の倍数、Yは857の倍数となります。Yは3桁の整数より、Y=857、従ってX=142。
以下、同様、