問題[平面図形]
|
|
|
|
|
|
半径が100円玉の半径の10倍ある大きな円があります。 |
|
|
|
|
|
解答例1[10-1]
| とらいしくるさん、ちこりんさん、kunioさん、ぺんこさん、智乃介さん、 たかのりさん、浜直君さん、吉田貴法さん、ミックケリーさん、Nなヒトさん、 tomhさん、ふじさきたつみさん、東羽衣の政幸さん、elmotitiさん、まるケンさん、 森よしさん、川村 高雅さん、やまやまさん、、他 |
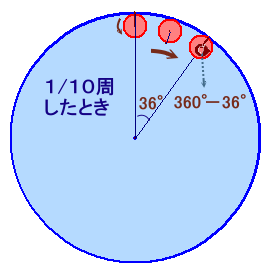
[アニメON]を押すと 100円玉が1/10周だけ回転するようすをアニメで表示します。
100円玉を大きな円の内側を右回りに転がすと、100円玉は逆の左回りに回転します。
100円玉が1/10周したとき、(360−36)度だけ回転するので、
1周すると(360度×10−360度)=360度×9、すなわち9回転することになります。答 9回転
以上
解答例2 [図を書いて解く、私が書くまでもないが、内側と外側の違い]
| エニグマさん、モトヤさん、塾教師さん、kasamaさん、パリンさん、 neoさん、大岡 敏幸さん、健太さん、 ピーターラビットさん、HAJIさん、他 |
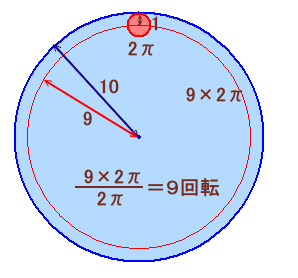
100円玉の半径を1とすると、100円玉の中心は半径9の円周を1周するので、
移動距離=9×2π、
これに対して100円玉の外周は2πなので、
回転数=(9×2π)/(2π)=9回転
することになります。