第９１問の解答

問題［空間図形]

問題図

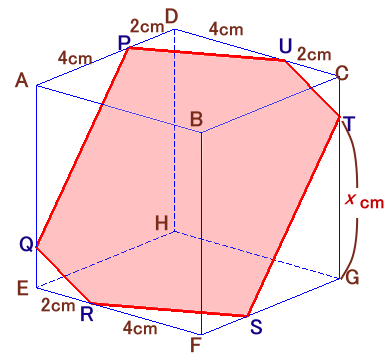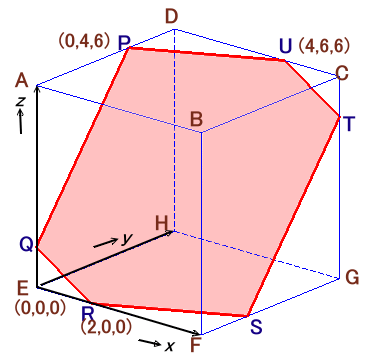
図は1辺が６cmの立方体ABCD-EFGHを平面PQRSTUで切断したものです。
AP＝DU＝FR＝4cmとなるように切断したとき、GTは何cmになりますか？

解答例１[相似,、延長、延長して相似 、STの傾きに着目]

Ｋｎｉｇｈｔさん、川村　高雅さん、ぺんこさん、こえだ§さん、浜直君さん、 長野　美光さん、みかんさん、ペンギンさん、 きょろ文さん、モトヤさん、ほげさん、mhayashiさん、吉田貴法さん、 　光希魔宇数（ミッキーマウス？）さん、HAJIさん、パリンさん、川村朗さん、neoさん、他　多数

UP、QR、STの交点をI、J、Kとします。

参考図１

これらは同一平面上にあるため、B、A、IとB、F、JおよびB、C、Kは、それぞれ一直線上に並んでいます。

まず、△UDPと△IAPが相似で相似比＝DP：AP＝１：２より、
　IA＝UD×２＝８cm。

次に、△KUCと△PIAが相似で相似比＝UC：IA＝１：４より、
　KC＝PA×１/４＝１cm。

また、△IBJと△RFJが相似で相似比＝IB：RF＝７：２より、
　BF：FJ＝５：２、
よって、
　FJ＝BF×２/５＝２．４cm。

そして、△KCTと△KBJが相似で相似比＝KC：KB＝１：７より、
　CT＝BJ×１/７＝１．２cm。

よって、
　GT＝CG−CT＝４．８cm
と求まります。

なお、PQ、RS、TUの交点を求めても同様に求まります。

答　４．８cm

以上

解答例２ [方程式で、座標]

　世之介さん、信三さん、tomhさん、 kasamaさん、ハラギャーテイさん、 他  

Eを原点として、EFをｘ軸、EHをｙ軸、およびEAをｚ軸とします。

参考図２

平面の方程式を、ax＋by＋cz＝1とすると、３点R(2,0,0)、P(0,4,6)、U(4,6,6)を通るので、
　2a＝1
　4b＋6c＝1
　4a＋6b＋6c＝1
が成り立つ。

これを解いて、a＝1/2、b＝−1、c＝5/6を得る。
平面はT(6,6,z)も通るので、　1/2×6−1×6＋5/6×z＝1より、
　ｚ＝24/5＝４．８cm
と求まります。