問題[推理( 覆面算)]
|
|
|
|
|
|
|
 |
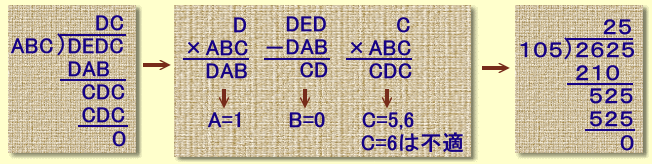
左の式のA〜Eは、0から9までのいずれかの、異なる数字を表わしています。 この式で割る数にあたるABCは何か、求めて下さい。 |
|
|
|
|
|
|
解答例1[A,B,C 、まず,AとBを出してから、順番にやった、まずBをだしてから、まずCを当てはめてから・・・]
| まるケンさん、kunioさん、アラちゃんさん、namaさん、Yyukomamaさん、 Happyさん、shiaroさん、 いさん、川村 高雅さん、浜直君さん、川村朗さん、 caniさん、モトヤさん、辻さん、ちこりんさん、tomhさん、 パリンさん、HAJIさん、優太さん、ショウさん、elmotitiさん、 ルナさん、kasamaさん、SSSさん、forestさん、かず。さん、 パァ〜子さん、 きょろ文さん、ピロシさん、とらいしくるさん、鳳 奥人さん、ゆうしゃさん、 あまれっとさん、みかんさん、信三さん、大岡 敏幸さん、りかさん、他 多数 |
どの順番で求めても大差ありませんので、ここではA、B、Cの順に求めてみましょう。
(A) 最初の割り算の結果より、D×ABC=DAB が成り立ちます。
D×Aの計算ではケタ上がりしていません。
A>1ならD×A>Dとなり不適、よってA=1と求まります。(B) 次の引き算の結果より、DED−DAB=CD が成り立ちます。
1の位の計算ではD−B=Dなので、B=0と求まります。(C) 最後の割り算の結果より、C×ABC=CDC が成り立ちます。
C×Cの計算結果の1の位が同じCになっています。
0から9までの整数でこのようになるのは、C=0、1、5、6の4つです。
C=0のとき、CDCではCが先頭の数字になっているので不適。
C=1のとき、C×ABC=ABCとなり、ABC≠CDCなので不適。
C=5のとき、C×ABC=5×105=525となり、D=2となります。
よって、DED=DAB+CD=210+52=262となり、E=6となります。
これらを元の割り算の各数字にあてはめてみると、題意を満たすことが分かります。C=6のとき、C×ABC=6×106=536となり、D=3となります。
よって、DED=DAB+CD=310+63=373となり、E=7となります。
ところが、D×ABC=3×126=378≠DABなので不適。以上から、ABC=105と決まります。
答 105
以上