問題[平面図形]
|
|
|
|
|
|
|
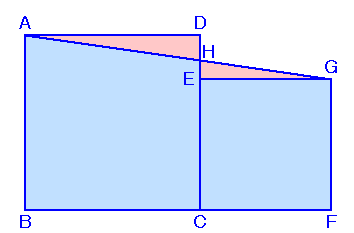 |
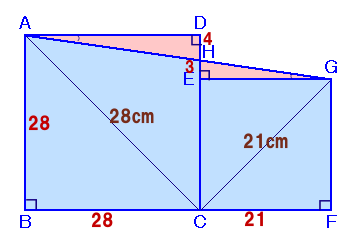
左図の正方形ABCDおよびECFGの対角線の長さは、それぞれ28cmと21cmです。 斜線部分の面積は合わせて何cm2ありますか。 |
|
|
|
|
|
|
解答例1[比、面積比 、対角線から長さの比を求めて面積比、1辺の長さが28と21の正方形で同じ図を書いて、相似→面積を25Sとおく]
| ヌオさん、HAJIさん、浜直君さん、大岡 敏幸さん、ショウさん、 caniさん、ぺんこさん、みかんさん、 川村 高雅さん、shiaroさん、吉田貴法さん、長野 美光さん、tomhさん、 塾教師さん、 きょろ文さん、kasamaさん、まりも母さん、ゴンともさん、 大地のパパさん、まるケンさん、 辻。さん、他 多数 |
どの方法もほぼ同じなので、ここでは分かりやすく辺の長さを28と21の正方形としてまず考えてみましょう。
△AHDと△GHEは相似な直角三角形で、相似比は28:21=4:3。
よって、
DH=DE×4/7=7×4/7=4、
EH=DE×3/7=7×3/7=3。従って、
△AHD+△GHE
=1/2×28×4+1/2×21×3
=87.5ある正方形と、その対角線を一辺とする正方形の面積比は1:2なので、
△AHD+△GHE
=87.5×1/2
=43.75cm2
と求まります。答 43.75cm2
以上