第９５問の解答

問題［整数の性質]

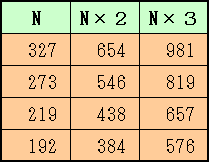
１９２を２倍すると３８４に、３倍すると５７６になり、もとの 整数を含めると 、１９２、３８４、５７６というように、１〜９の数字が１回ずつ登場します。

同じように３桁の整数で、もとの 整数と２倍、３倍した整数の各ケタの数字の中に 、１〜９の数字が１回ずつ登場するようなもののうち、一番大きい整数を求めなさい。

解答例１[範囲を決めてしらみつぶし]

みかんさん、智乃介さん、shiaroさん、川村　高雅さん、吉田佳薫さん、 ドクター算数さん、吉田貴法さん、ティーハラさん、浜直君さん、たこ焼きｂさん、 紗月さん、ぺんこさん、ゆうしゃさん、あまれっとさん、TOMMYさん、 caniさん、ハムアチパパさん、かず。さん、トシえもんさん、森よしさん、 tomhさん、優太さん、パリンさん、kasamaさん、川村朗さん、 やまけんさん、青二才さん、 　他 多数

３倍しても３桁になる整数は３３３以下になります。

３３０〜３３３は百の位と十の位の数字が同じなので不適。
３２９以下の数字について、２倍、３倍の数字を計算し題意に適すものを探していきます。

すると、題意に適する整数は１９２、２１９，２７３、３２７の４個であることが分かります。
このうち最大のものは３２７です。

参考図１

答　 ３２７

以上

（その他の解法）