問題[平面図形]
|
|
|
|
|
|
|
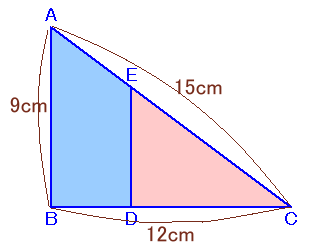 |
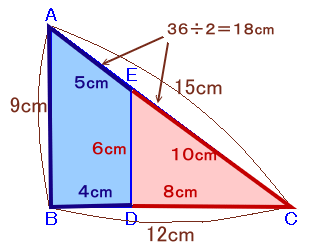
AB=9cm、BC=12cm、CA=
15cmの直角三角形があります。 |
|
|
|
|
|
|
解答例1[EC+CDは△ABCの周の半分 、EDは一致しているので]
| C-Dさん、寺脇犬さん、みかんさん、智乃介さん、HAJIさん、 長野 美光さん、まるケンさん、パァ〜子さん、nakatukahirohikoさん、川村朗さん、 ショウさん、森よしさん、優太さん、 きょろ文さん、ゆうしゃさん、ゴンともさん、他 |
台形ABDEと△EDCは辺DEが共通なので、DEを除く周りの長さが等しいことになります。
従って、
AE+AB+BD=EC+DCところが、
(AE+AB+BD)+(EC+DC)
=△ABCの周りの長さ
=9+12+15=36cmよって、
AE+AB+BD=EC+DC=18cm ・・・ (1)ところが、△EDCは△ABCと相似なので、
ED:DC:EC=AB:BC:DC=3:4:5よって、
ED=18×3/(4+5)=6cm
DC=18×4/(4+5)=8cm
EC=18×5/(4+5)=10cm従って、
台形ABDE
=1/2×(AB+ED)×BD
=1/2×(9+6)×4
=30cm2
と求まります。答 30cm2
以上
解答例2 [CD+CEとDB+EAの差が9cm、ピラミッドより面積比の利用]
| masasiさん、光希魔宇数(ミッキーマウス?)さん、もありすさん、他 |
(EC+DC)と(AE+AB)の和=AC+BC=27cm、差=AB=9cmより、
EC+DC=(27+9)÷2=18cm、
AE+AB=(27−9)÷2=9cm。よって、△ABCと△EDCの相似比=(AC+BC):(EC+DC)=27:18=3:2。
△ABCと△EDCの面積比=9:4、
△ABCと台形ABDEの面積比=9:5。よって、
台形ABDE
=△ABC×5/9
=(1/2×9×12)×5/9
=30cm2
と求まります。
解答例3 [3:4:5の利用、比と方程式]
| 浜直君さん、TOMMYさん、陵さん、龍さん、 いさん、貴さん、 有無相生さん、大岡 敏幸さん、kasamaさん、パリンさん、tomhさん、他 |
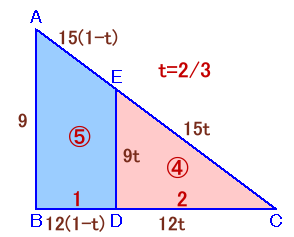
△ABCと△EDCの相似比を1:tとします。
ED=9t、DC=12t、EC=15t、AE=15(1−t)、BD=12(1−t)
となります。従って、
15(1−t)+9+12(1−t)+9t=15t+9t+12t
これより、t=2/3を得ます。よって、△ABCと△EDCの面積比は1:t2=1:4/9、
従って、△ABCと台形ABDEの面積比=1:1−t2=1:5/9以下、同様。