第９８問の解答

問題［平面図形]


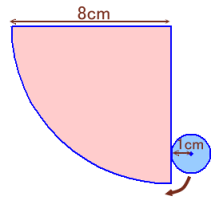		半径８cmの4分の1円の周りを、半径１cmの円が１周します。このとき、円が通った部分の図形の面積は何cm²になりますか？

解答例１[図を書いてそれぞれ計算、全体から半径８ｃｍの1/4円を引く]

山口勇太郎さん、ショウさん、AYAKAさん、ゴンともさん、HAJIさん、モトヤさん、みかんさん、エガオヲミセテさん、大岡さん、浜直君さん、優太さん、まるケンさん、kasamaさん、アラちゃんさん、パリンさん、tomhさん、ka-ruさん、もありすさん、智乃介さん、 TOMMYさん、川村　高雅さん、RDさん、青山はなこさん、ゆうしゃさん、 lasalleさん、たけのこさん、ちずさん、紗月さん、グレープフルーツさん、高砂さん、たけのこさん、他

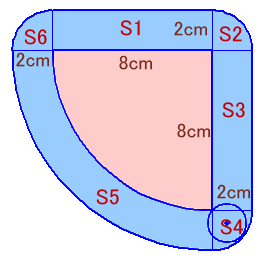
円が通ったあとにできる図形は、4分の1円の外周および外周から２ｃｍ（円の直径）だけ離れた点の集まりで囲まれた領域になります。

Ｓ₁＝Ｓ₃＝８×２＝１６cm²

Ｓ₂＝Ｓ₄＝Ｓ₆＝３．１４×２²×１/４＝３．１４cm²

Ｓ₅＝３．１４×１０²×１/４－３．１４×８²×１/４＝２８．２６cm²

よって、
　求める面積
＝Ｓ₁×２＋Ｓ₂×３＋Ｓ₅
＝１６×２＋３．１４×３＋２８．２６＝６９．６８cm²
と求まります。

答　 ６９．６８cm²

以上

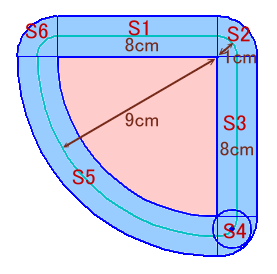
解答例２ [円の中心の移動距離を求めて×２㎝、円の直径が大事、周囲の長さX幅＋円の面積]

きょろ文さん、吉田貴法さん、ちこりんさん、Nなヒトさん、ミト清さん、たけのこさん、橋本和大さん、信三さん、他

求める図形は、幅が２ｃｍで長さが円の中心の移動距離となる帯と考えることができます。

移動距離＝８×２＋３．１４×２×１/４×３＋３．１４×１８×１/４＝３４．８４ｃｍ
よって、面積＝３４．８４×２＝６９．６８cm²
と求まります。


	円が通ったあとにできる図形は、4分の1円の外周および外周から２ｃｍ（円の直径）だけ離れた点の集まりで囲まれた領域になります。Ｓ₁＝Ｓ₃＝８×２＝１６cm² Ｓ₂＝Ｓ₄＝Ｓ₆＝３．１４×２²×１/４＝３．１４cm² Ｓ₅＝３．１４×１０²×１/４－３．１４×８²×１/４＝２８．２６cm² よって、　求める面積＝Ｓ₁×２＋Ｓ₂×３＋Ｓ₅ ＝１６×２＋３．１４×３＋２８．２６＝６９．６８cm² と求まります。答　６９．６８cm² 以上


	求める図形は、幅が２ｃｍで長さが円の中心の移動距離となる帯と考えることができます。移動距離＝８×２＋３．１４×２×１/４×３＋３．１４×１８×１/４＝３４．８４ｃｍよって、面積＝３４．８４×２＝６９．６８cm² と求まります。