問題[規則性]
|
|
|
|
|
|
来年こそは、算数を極めようと心に決めたA君とB君は、TORA先生に計算プリントを決まったペースで提出することにしました。
では2人がTORA先生に提出したプリントの枚数が初めて同じになるのは、1月何日のことでしょうか? |
|
|
|
|
|
解答例1[表にした 、全部書く、カレンダーに書き込む]
| taishiさん、たけのこさん、川村さん、みかんさん、紫亜呂さん、 C-Dさん、ゆうしゃさん、智乃介さん、とらいしくるさん、 高砂さん、ピーターラビットさん、kasamaさん、tomhさん、ショウさん、 パリンさん、 橋本和大さん、ふうきさん、HAJIさん、三浦晃祐さん、ミト清さん、 大岡 敏幸さん、優太ぱぱさん、吉田貴法さん、伸樹さん、橋本和大さん、塾講師さん、NARUTOさん、他 |
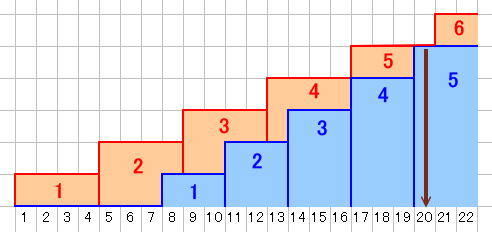
表またはカレンダーに書き込んでいくと、
A : 1月17日〜21日 ・・・ 5枚
B : 1月20日〜23日 ・・・ 5枚
となって、A、Bとも1月20日に5枚提出したことになり、これが初めて提出数が同じになる日と分かります。
答 1月20日
以上
解答例2 [数列っぽく]
| mhayashiさん、他 |
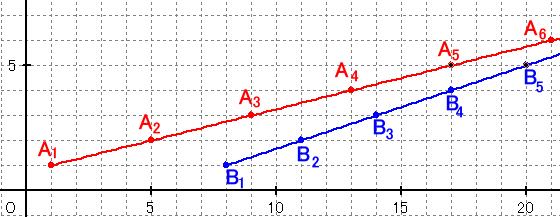
A、B君がn枚目のプリントを提出した日をAn、Bnとします。
A君は、1日から始めて4日ごとに提出するので、An=4(n−1)+1=4n−3
B君は、8日から始めて3日ごとに提出するので、Bn=3(n−1)+8=3n+5
と表せます。B君のほうが後から提出し始めるので、2人の提出枚数が同じになるには、
An+1>Bn≧An従って、
4(n+1)>3n+5≧4n−3
8≧n>4 ・・・ (1)
となります。始めて同じになる日は、(1)を満たす最小の整数だから
n=5
となります。A6=21>B5=20≧A5=17
より、20日が求める日と分かります。
(その他の解法)
- 計算機プログラム ・・・ ハラギャーテイさん、masasiさん