第1問(2)の解答
1.問題
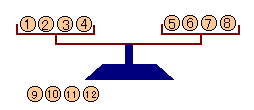
| (1)12個のおもりがあります。このうち、1個だけ他のおもりと重さが異なるものがあります。天秤を利用して何回かおもりを量り、どのおもりが他と異なるかを見つけて下さい。 さて、おもりを量る回数をできるだけ少なくするとして、最大何回量ればいいでしょうか。 また、その具体的な量り方を考えて下さい。 (2)7回まで量ることができるとします。このとき、最大何個のおもりのなから1個だけある重さの異なるものを見つけることができるでしょうか。 |
2.設問(2)
一般におもりがm個のとき、いずれかのおもりが重いあるいは軽いのm×2通り可能性があります。ところが、n回はかることで、3n通りの状態を区別することができるので、m×2≦3nとなります。3nは奇数なので、結局m≦(3n−1)/2となります。
ところが、効率的にはかることで、(3n−1)/2個のおもりの中から異なるものを判定することができることを示せますので、最大個数は(3n−1)/2個となります。

n=7のときは、(37−1)/2=1093個です。
一般には数学的帰納法で証明できますが、ここでは7個の場合を具体的に示してみましょう。
(おもりが7個の場合)
1回目に左右に載せることができる最大個数mは、もし天秤が傾いたときにm×2通りの場合が考えられ、残りの6回で36=729通りの状態が判定できることからm×2≦729、m≦364個となります。
・1回目:1〜364のおもりを左、365〜728のおもりを右に載せ(計728個)、729〜1093(365個)を残します。
・左が重いとき:1〜364が重いか365〜728が軽い(728通り)
・右が重いとき:1〜364が軽いか365〜728が重い(728通り)
・釣り合うとき:729〜1093が異なる(365通り)・・・「1回目に釣り合った場合」へ・2回目:
・左の天秤:重い可能性のある364個のおもりのうち122個と軽い可能性のある364個のおもりのうち121個。
・右の天秤:重い可能性のある364個のおもりのうち122個と軽い可能性のある364個のおもりのうち121個。
・残す:重い可能性のある364個のおもりのうち120個と軽い可能性のある364個のおもりのうち122個・左が重いとき:122個のどれかが重いか121個のどれかが軽い(243通り)
・右が重いとき:122個のどれかが軽いか121個のどれかが重い(243通り)
・釣り合うとき:122個および120個ののどれかが異なる(重いか軽いかは分かる)(242通り)
・3回目:(以下、前に釣り合ったときは個数が1個少なくてすむ)
・左の天秤:122個のおもりのうち41個と121個のおもりのうち40個。
・右の天秤:122個のおもりのうち41個と121個のおもりのうち40個。
・残す:122個のおもりのうち40個と121個のおもりのうち41個。・左が重いとき:41個および40個ののどれかが異なる(重いか軽いかは分かる)(81通り)
・右が重いとき:41個および40個ののどれかが異なる(重いか軽いかは分かる)(81通り)
・釣り合うとき:41個および40個ののどれかが異なる(重いか軽いかは分かる)(81通り)・4回目:
・左の天秤:41個のおもりのうち14個と40個のおもりのうち13個。
・右の天秤:41個のおもりのうち14個と40個のおもりのうち13個。
・残す:41個のおもりのうち13個と40個のおもりのうち14個。・左が重いとき:14個および13個ののどれかが異なる(重いか軽いかは分かる)(27通り)
・右が重いとき:14個および13個ののどれかが異なる(重いか軽いかは分かる)(27通り)
・釣り合うとき:14個および13個ののどれかが異なる(重いか軽いかは分かる)(27通り)・5回目:
・左の天秤:14個のおもりのうち5個と13個のおもりのうち4個。
・右の天秤:14個のおもりのうち5個と13個のおもりのうち4個。
・残す:14個のおもりのうち4個と13個のおもりのうち5個。・左が重いとき:5個および4個ののどれかが異なる(重いか軽いかは分かる)(9通り)
・右が重いとき:5個および4個ののどれかが異なる(重いか軽いかは分かる)(9通り)
・釣り合うとき:4個および5個ののどれかが異なる(重いか軽いかは分かる)(9通り)・6回目:
・左の天秤:5個のおもりのうち2個と4個のおもりのうち1個。
・右の天秤:5個のおもりのうち2個と4個のおもりのうち1個。
・残す:5個のおもりのうち1個と4個のおもりのうち2個。・左が重いとき:2個および1個ののどれかが異なる(重いか軽いかは分かる)(3通り)
・右が重いとき:2個および1個ののどれかが異なる(重いか軽いかは分かる)(3通り)
・釣り合うとき:1個および2個ののどれかが異なる(重いか軽いかは分かる)(3通り)・7回目:
・左の天秤:2個のおもりのうち1個。
・右の天秤:2個のおもりのうち1個。
・残す:1個のおもりのうち1個。・左が重いとき:1個が異なる(重いか軽いかは分かる)
・右が重いとき:1個が異なる(重いか軽いかは分かる)
・釣り合うとき:1個が異なる(重いか軽いかは分かる)
(1回目に釣り合った場合)残り365個
・2回目:残り365個のなかから243個のおもりを左、正しいおもりを243個右に載せ、122個を残します。
・左が重いとき:243個のどれかが重い
・右が重いとき:243個のどれかが軽い
・釣り合うとき:122個のどれかが異なる・・・「2回目に釣り合った場合」へ
・3回目:異なる(重いか軽いかは分かる)243個のなかから81個のおもりを左、81個を右に載せ、81個を残します。(3分割法と呼ぶ)
・左が重いとき:81個のどれかが異なる(重いか軽いかは分かる)
・右が重いとき:81個のどれかが異なる(重いか軽いかは分かる)
・釣り合ったとき:81個のどれかが異なる(重いか軽いかは分かる)以下、個数を3分の1づつに絞っていけるので、7回目で異なるおもりとそれが重いのか軽いのかまでが判定できる。
(2回目に釣り合った場合)残り122個
・3回目:残り122個のなかから81個のおもりを左、正しいおもりを81個右に載せ、41個を残します。
・左が重いとき:81個のどれかが重い(以下3分割法により後4回で分かる)
・右が重いとき:81個のどれかが軽い(〃)
・釣り合うとき:41個のどれかが異なる・・・「3回目に釣り合った場合」へ
(3回目に釣り合った場合)残り122個
・4回目:残り41個のなかから27個のおもりを左、正しいおもりを27個右に載せ、14個を残します。
・左が重いとき:27個のどれかが重い(以下3分割法により後3回で分かる)
・右が重いとき:27個のどれかが軽い(〃)
・釣り合うとき:14個のどれかが異なる・・・「4回目に釣り合った場合」へ
(4回目に釣り合った場合)残り14個
・5回目:残り14個のなかから9個のおもりを左、正しいおもりを9個右に載せ、5個を残します。
・左が重いとき:9個のどれかが重い(以下3分割法により後2回で分かる)
・右が重いとき:9個のどれかが軽い(〃)
・釣り合うとき:5個のどれかが異なる・・・「5回目に釣り合った場合」へ
(5回目に釣り合った場合)残り5個
・6回目:残り5個のなかから3個のおもりを左、正しいおもりを3個右に載せ、2個を残します。
・左が重いとき:3個のどれかが重い(以下3分割法により後1回で分かる)
・右が重いとき:3個のどれかが軽い(〃)
・釣り合うとき:2個のどれかが異なる・・・「6回目に釣り合った場合」へ
(6回目に釣り合った場合)残り5個
・7回目:残り2個のなかから1個のおもりを左、正しいおもりを1個右に載せ、1個を残します。
・左が重いとき:左の1個が重い
・右が重いとき:左の1個が軽い
・釣り合うとき:残した1個が異なる(重いか軽いか分からない)
以上