第２問（２）の解答

---

１．問題

（１）７個のおもりがあります。重さは、１ｇ、３ｇ、９ｇ、２７ｇ、８１ｇ、２４３ｇ、７２９ｇです。天秤とこれらのおもりを利用して１ｇから１０９３ｇまでの連続した整数に対する重さの全てをはかることができます。このことを説明して下さい。 （２）７７７ｇをはかるには、天秤におもりをどのように載せればよいでしょうか

---

２．設問（２）：解答例１（ありさのお父さん、大岡敏幸さん）

１≦X≦１０９３に対して、Xを３進数で表します。
　　X＝B0＋B1×３¹＋B2×３²＋B3×３³＋B4×３⁴＋B5×３⁵＋B6×３⁶
とする。ただし、B0、・・、B6＝0，1，2である。

ここで、１＋１×３¹＋１×３²＋１×３³＋１×３⁴＋１×３⁵＋１×３⁶＝１０９３だからB6は０または１となります。

0≦n≦6に対し、
　Bn＝０または１のときはAn＝Bn、
　Bn＝２のときはAn＝−１、Bn+1＝Bn＋１とします。
２×３ⁿ＝１×３ⁿ⁺¹−１×３ⁿであるから、この操作によって
　　X＝A0＋A1×３¹＋A2×３²＋A3×３³＋A4×３⁴＋A5×３⁵＋A6×３⁶
と表すことができる。ただし、A0、・・、A6＝−１，０，１

このとき、B6＝２となり、
　X＝A0＋A1×３¹＋A2×３²＋A3×３³＋A4×３⁴＋A5×３⁵＋A6×３⁶＋１×３⁷
となることななないことを示す。もしそうなったとしたら、
　−１０９３＝−１ −１×３¹ −１×３² −１×３³ −１×３⁴ −１×３⁵ −１×３⁶
　≦A0＋A1×３¹＋A2×３²＋A3×３³＋A4×３⁴＋A5×３⁵＋A6×３⁶
よって、１×３⁷−１０９３＝２１８７−１０９３＝１０９４≦Xとなり矛盾。

では、X＝７７７のときを考えましょう。X＝７７７を３進数で表すと、
　X＝１００１２１０（３進数）となります。
そこで、上記操作を行うと、X＝１０１１１１０となります。ただし、１は−１を表します。
すなわち、
　　X＝0＋１×３¹−１×３²−１×３³＋１×３⁴＋０×３⁵＋１×３⁶
　　　＝３−９−２７＋８１＋７２９

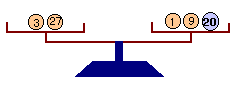
よって、３，８１，７２９ｇを左の天秤に、９，２７ｇを右に載せると７７７ｇのものを右の天秤に載せて量ることができます。

答：３，８１，７２９ｇを左の天秤に、９，２７ｇを右に載せる

以上

---

３．設問（２）：解答例２（中村明海さんによる）

X＝７７７，Y=X+１０９３＝１８７０とし、Ｙを３進数で表すと、
　　Y＝２１２００２１（３進数）
X＝Y−１０９３＝２１２００２１（３進数）-１１１１１１１（３進数）＝１０１１１１０（３進数）
　＝0＋１×３¹−１×３²−１×３³＋１×３⁴＋０×３⁵＋１×３⁶
　＝３−９−２７＋８１＋７２９

答：３，８１，７２９ｇを左の天秤に、９，２７ｇを右に載せる

以上

---