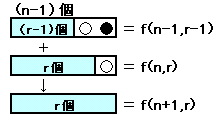第3問の解答
1.問題
| 10個の碁石が1列に並んでいます。 (1)このうち、連続した碁石を選ぶ選び方は何通りでしょう。 (2)どの碁石も隣り合わないように選ぶ選び方は何通りでしょう。 |
2.設問(1):解答例1(ありさのお父さん、他)
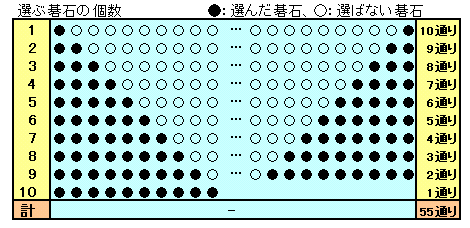
選ぶ碁石の個数が増えるに従って、選び方が減ってきます。
答:55通り
以上
3.設問(2):解答例1(三好知之さん他)
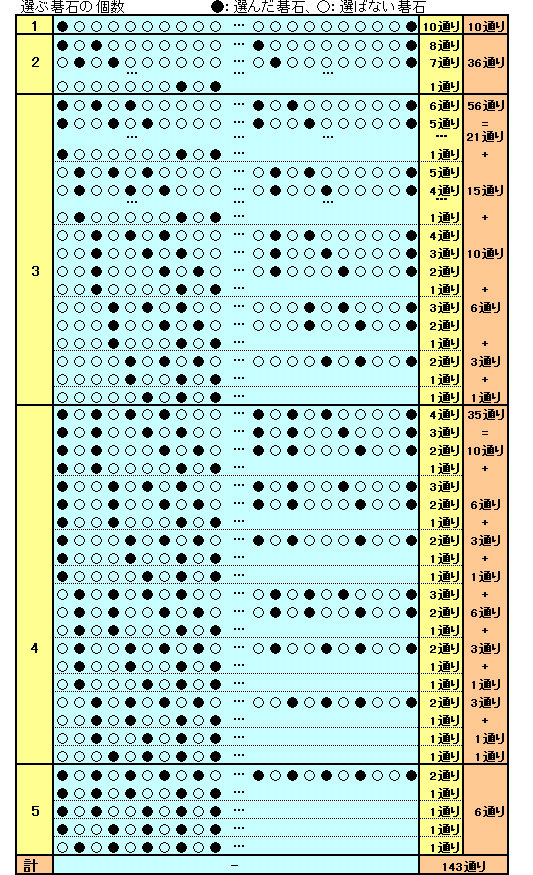
下表のように数えると合計143通りとなります。
以上
4.設問(2):解答例1(kuri他)
碁石がn個あって、そのうちr個を選ぶ選び方をf(n,r)通りとします。
f(n,1)=n,f(n1,r)=1は明らか。ただし、n1=2*r-1。
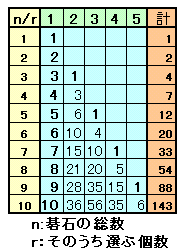
また、図1よりf(n+1,r)=f(n,r)+f(n-1,r-1)となるので、これから順に求めていくと表1のごとく求まり、碁石が10個のときの選び方総数は143通りとなる。
図1
表1
なお、碁石がn個の時の選び方総数をg(n)とすると、g(n+1)=g(n)+g(n-1)+1となっていることに注意。
これより、h(n)=g(n)+1とおくと、h(n+1)=h(n)+h(n-1)となり、h(n)がフィボナッチ数列として一般式を求めることが出来る。
5.設問(2):解答例2
下図のように、選んだ碁石(最後の碁石を除く)の右側には必ず選ばない碁石があるので、これをペアで考えると、結局n-r+1の碁石からr個選ぶ選び方f(n,r)=n-r+1Crに等しいことが分かる。
これより求めたf(n,r)は、表1と合致する。
6.設問(2):解答例3(ありさのお父さん、中村明海さん)
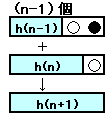
碁石がn個の時の選び方総数をg(n)とする。 碁石を全く選ばない場合の1通りを含めて考えることとし、h(n)=g(n)+1とすれば、左図より、h(n+1)=h(n-1)+h(n)を得るので、h(n)はフィボナッチ数列となる。
h(1)=2、h(2)=3より順次計算していけば、h(10)=144となるので、g(10)=h(10)-1=143通りとなる。
以上