第４問の解答

１．問題

左図のような縦８×横１０のマス目があります。
今、赤いボールをＣの角のマス目から４５度の角度で動かしていくことにしました。ボールは壁にぶつかると反射して、やはり４５度の角度ですすんでいきます。

（１）さて、ボールは一体何回壁にぶつかって角に達するでしょうか。
（２）また、その角はＡ、Ｂ、Ｃ、Ｄのどれでしょうか。
（３）縦ｍ×横ｎ（ｍ、ｎ：正の整数）のときは、何回壁にぶつかって、どの角に到達するでしょうか。

（注）ボールはマス目の上を動きますので、反射の仕方に注意して下さい。

２．設問（１）、（２）：解答例

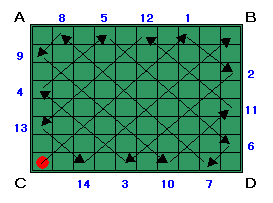
実際に進めてみると、左図のように１４回壁にぶつかりＢに到達します。

　　　答：（１）１４回
　　　　　（２）Ｂ

以上

３．設問（３）：解答例

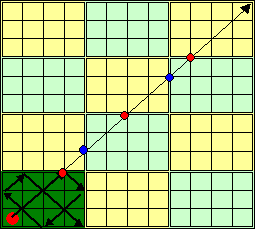
マス目上を進んでいく場合の反射の仕方は分かりにくいので、格子上を進む場合を考えてみましょう。

参考図２

上図のように、縦４×横５のマス目を進むことと、縦３×横４のマス目の格子上を進むことは同じことになります。

次に、ボールは縦方向に格子を３つだけ進むたびに上下の壁にぶつかり、横方向に４つ進むたびに左右の壁にぶつかることが分かります。

そこで、ボールの進む方向に延長してみると、角に到達するのは、ボールの進んだ格子の数が、３の倍数かつ４の倍数、すなわち１２個進むこととなります。

4-3.gif (3943 バイト)

このとき、縦方向には、縦３×横４のマス目の１２／３＝４倍進むことになるので、壁には４－１＝３回ぶつかります。同様に横方向には縦３×横４のマス目の１２／４＝３倍進むことになるので、壁には３－１＝２回ぶつかります。

一般に縦ｍ×横ｎのマス目の場合はどうなるでしょうか。
さきほど同様、縦（ｍ-1)×横（ｎ-1)のマス目の格子上を進むことを考えます。
m-1、n-1の最小公倍数をｓ、m-1＝ｔ×ｓ、n-1＝ｕ×ｓとします。

すると、縦方向には縦（ｍ-1)×横（ｎ-1)のマス目のｔ倍だけ進むことになり、ｔ－１回壁にぶつかります。横方向にはｕ倍進むことになり、ｕ－１回壁にぶつかります。

従って、合計（ｔ＋ｕ－２）回壁にぶつかります。

また、どの角にぶつかるかを考えてみましょう。
ｔが奇数のときはボールは上側の壁の上にあり、偶数のときは下側にあります。
また、ｕが奇数のときはボールは右側の壁の上にあり、偶数のときは左側にあります。

従って、
　１）ｔが奇数、ｕが偶数のとき、Ａに到達
　２）ｔが奇数、ｕが奇数のとき、Ｂに到達
　３）ｔが偶数、ｕが奇数のとき、Ｄに到達
することが分かります。

なお、ｓが最小公倍数なのでｔ，ｕは互いに素となり、ともに偶数となることはありません。

さて、設問（１）、（２）の場合にこの結果を適用してみましょう。
m=8,n=10ですから、m-1=7,n-1=9となり、最小公倍数は７×９＝６３となります。
さらに、ｔ＝６３／７＝９、ｕ＝６３／９＝７より壁にぶつかるのは、ｔ＋ｕ－２＝９＋７－２＝１４回、またｔ＝９，ｕ＝７ともに奇数ですからＢに到達することになります。

以上