第5問の解答
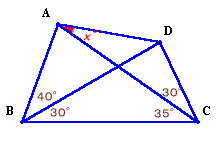
1.問題
 |
|
2.解答例1(ありさのお父さん、たなかさん、Asamiさん、kuri)
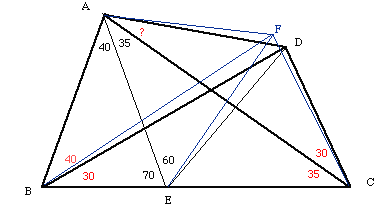
辺BC上にAB=AEとなるようにEをとると、三角形AEDが正三角形になりx=25°であることが分かります。
しかしながら、三角形AEDが正三角形となることを直接示すことは難しいので、間接的に示します。皆さん、ほぼ同様な解法で求めておられます。
下記の解法はありさのお父さんによる方法です。
AEを一辺とする正三角形AEFをつくります。
まず、AB=AEより三角形ABEは二等辺三角形となり、∠AEB=∠ABE=70°、∠BAE=180−70×2=40°となります。
従って、∠EAC=∠BAC−40=75−40=35°となるので、三角形EACは二等辺三角形、よってAE=EC。
次に、EF=AE=ECより三角形ECDは二等辺三角形となり、∠FEC=180−70−60=50°であるから、∠ECF=(180−50)/2=65°=∠ECD。よって、FはCD上またはその延長線上にあることが分かる。
今度は、三角形ABFを考えます。
AB=AE=AFだからABFは二等辺三角形となり、∠ABF=∠AFB=∠AFE−∠BFE=60−20=40°、よってFは辺BFまたはその延長線上にあることとなる。以上から、Fは結局Dに一致することが分かる。
よって、∠CAD=∠EAD−∠EAC=60−35=25°となります。
答:25°
以上