第６問の解答

---

１．問題

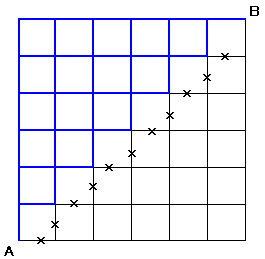
左図の縦６×横６のマス目および格子があります。 格子の線上をＡからＢに進む最短経路は何通りでしょうか？ ただし、×印のついたところは不通個所となっていますので通れません。

---

２．解答例１（ありさのお父さん、大岡さん、Ｋ．Ｋさん、三好知之さん、吉田和義さん、kuri）

出発点から順に，各交差点に（下と左の交差点の数字を足した）場合の数を書き込んで行くと最後のＢ点へは１３２通りとなることが分かります。

なお下図では、交差点から次の交差点までの線分上を通る場合の数を書いています。

答：１３２通り

以上

---

３．解答例２（清川育男さん、Ａｓａｍｉさん、たなかさん）：カタラン数による

（補題）縦ｍ×横ｎのマス目で制約のない場合の最短経路数はm+nＣmである。
	上に進むことをＮ、右に進むことをＥと表すと、最短経路は合計ｍ＋ｎ回進むうち、ｍ回を選んでそれをＮとし、残りをＥとすることと対応する。

まず、制約のない場合のＡからＢへ至る最短経路数は_６+６Ｃ_６＝_１２Ｃ_６＝９２４通りである。

次に、不通区間を通る場合の数を求めよう。
不通区間を通る場合（赤色線）は、上図の点線部分を横切ることとなる。
この経路を、点線を初めて横切った個所以降を点線と軸として対称に移動したもの（黄色）を考える。これは、ＡからＣへ至る制約のない最短経路の一つである。

逆にＡからＣへ至る制約のない最短経路の一つをとると、これも点線部分を必ず横切るので、点線を初めて横切った個所以降を点線と軸として対称に移動したものを考えると、これはＡからＢへ至る最短経路で不通区間を通る経路の一つとなる。

以上から、不通区間を通る場合の数は、結局ＡからＣへ至る制約のない最短経路の数と一致するので、_７+５Ｃ_５＝_１２Ｃ_５＝７９２通りとなる。

よって、求める制約ありの最短経路数は_１２Ｃ_６−_１２Ｃ_５＝９２４−７９２＝１３２通りとなる。

一般に縦ｎ×横ｎの場合は、_２ｎＣ_ｎ−_２ｎＣ_n-1＝_２ｎＣ_ｎ/(n+1)となります。（カタラン数）

なお、詳しくは、清川さんが紹介していただいた たなかさんの解答例を参照下さい。