第8問の解答
1.問題
図1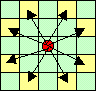 |
図2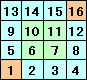 |
|
|
||
2.解答例1(中村明海さん、Asamiさん、清川育男さん、三好知之さん、たなかさん他)
上図のようにマス目を色分けすると、1回の移動でナイトは別の色のマス目に移ります。従って、同じ色のマス目へは偶数回、異なる色のマス目へは奇数回の移動で移れることが分かります。
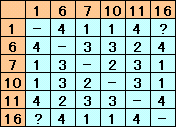
このことを念頭に置いて、移動すべき1,6,7,10,11,16の各マス目間の最小手数を求めます。結果は、下図の通り。
1から最初に移動するのは、7または10ですが、対象性を考慮して7のほうだけを考えても大丈夫です。 7からは、6または11 ・・・ 3手 (1) 10 ・・・ 2手 (2) の2通りが考えられます。(1)のとき:6の場合を考えます
11->10->16は2+3+1=6手,10->11->16は3+3+4=10手かかるので、前者が短手数で1からの合計手数は10手となります。(2)のとき:
6->11->16,11->6->16のいづれでも3+2+4=9手かかるので、1からの合計手数は12手となります。従って、最小手数は例えば1->7->6->11->10->16の10手と分かります。
答:10手
以上