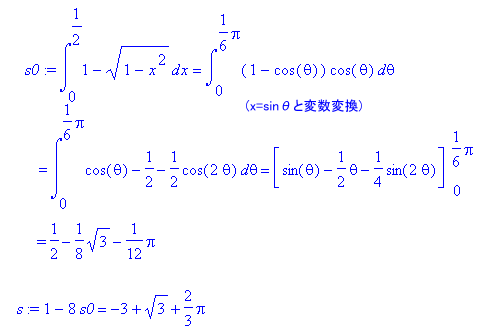第９問の解答

１．問題

問題図
左図のような半径が1cmの正方形ＡＢＣＤがあります。

今、頂点Ａを正方形の中に折り返した点をＡ’とします。
このように四隅を正方形の中に折り返した点の集まりが形作る図形の面積を求めて下さい。

(注)求める図形は、次のように考えて下さい。
隣り合う２辺例えばＡＢ、ＡＤ上の適当な点を結んだ直線を軸にして 正方形を折ります。そのとき頂点Ａが正方形のある部分Ａ’にくるわけですが、 軸をいろいろ変えたときＡ’の動いた軌跡がある図形になります。
同様に、Ｂ、Ｃ、Ｄについても動いた軌跡の図形を考えます。
求める図形は、これらをすべて合成したものです。

２．解答例１

参考図１

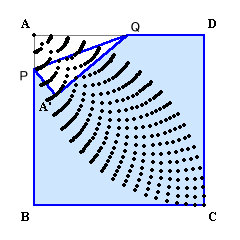
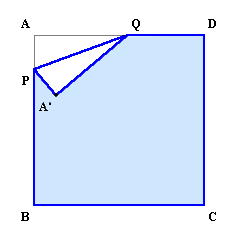
上図のようにＰ、ＱをＡＢおよびＡＤ上を動かしてみます。すると、Ａ’の軌跡はＢを中心とする４分の１円ＡＣおよびＤを中心とする４分の１円ＡＣの内部を動くことが予想されます。

8-3.gif (2232 バイト)

このことは次のようにして確かめることが出来ます。
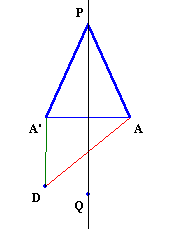
ＡとＡ’は直線ＰＱに関して対称になります。
Ｄは直線ＰＱに関してＡ’と同じ側にあるので、ＤＡ’≦ＤＡ。
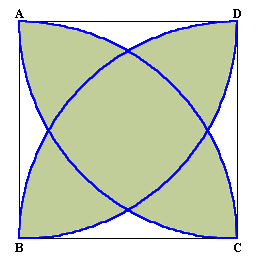
同様にして、ＢＡ’≦ＢＡ。

Ｂ、Ｃ、Ｄを折り返した場合も同様なので、結局下記のような図形となる。

参考図３

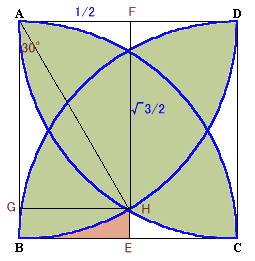
さて、この図形の面積を求めよう。（吉田和義さん他による）
参考図４
まず、朱色部分ＢＥＨの面積を求める。
ＢＥＨ＝長方形ＡＢＥＦ−三角形ＡＨＦ−円弧ＡＢＨ
　　　＝1×1/2−1/2×1/2×√３／２−π×１2／(30/360)
　　　＝1/2-√3/8-π/12
よって、
求める面積＝正方形ＡＢＣＤ−ＢＥＨ×８
　　　　　＝1-(1/2-√3/8-π/12)×８
　　　　　＝-3+√3+2/3π
答：-3+√3+2/3π cm2

（面積を積分で求める）

参考図５

　

以上