第12問の解答
1.問題
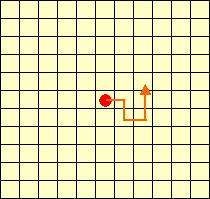
左図のような11×11のマス目があります。
中央のマス目から5歩だけ進めこととします。
ただし、進む方向は上下左右のみで、同じマス目を2度以上通ることはできません。(1)到達出来るマス目は何個あるでしょう。
(2)進む経路は延べ何通りあるでしょう。
2.解答例1(吉田和義さん、kuri)数え上げ
(設問1)
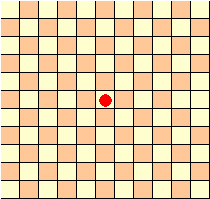
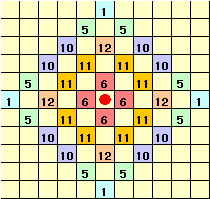
下図のように市松模様に色分けします。
1歩ごとに、色の異なるマス目に進むことが分かります。
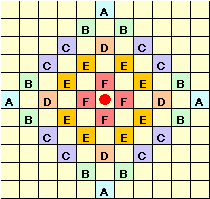
従って、中央のマス目と同じ色のマス目には奇数歩で、異なる色のマス目には偶数歩で進みます。よって、5歩で進めるマス目は下図のように36個あることが分かります。
(設問2)
対称性より、上図で同じ記号の場所への進み方は同数あります。
(1)A,B,C
これらのマス目へは最短でも5歩なので、各マス目への進み方は最短経路数となります。
A:(5+0)!/5!0!=1通り
B:(4+1)!/4!1!=5通り
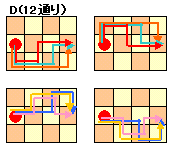
C:(3+2)!/3!2!=10通り(2)D
下図のように12通りあります。
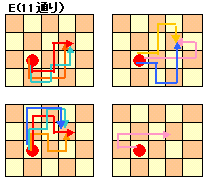
(3)E
下図のように11通りあります。
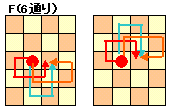
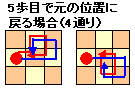
(4)F
下図のように6通りあります。
以上より、1×4+5×8+10×8+12×4+11×8+6×4=284通りとなります。
答:(1)36個 (2)284通り
以上
3.解答例2(ちゃめさん、清川育男さん、たなかさん)
(設問2)
最初に進むマス目は上下左右の4個所あります。
対称性より、最初に右側へ進む場合を考えれば、全体はその4倍ということになります。2歩目以降は、元のマス目には戻れないので進み方はそれぞれ3通り。
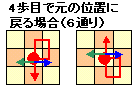
従って、3×3×3×3=81通りとなります。しかし、この中には同じマス目に進む場合の10通りが含まれますので、これらを除く必要があります。
従って、求める進み方は(81−10)×4=284通りとなります。
以上