第１３問の解答

１．問題

問題図
正三角形をさらにいくつかの正三角形に分割することを考えます。
左図では、正三角形を４等分していますが、分割後の正三角形は異なる大きさでも構いません。

（１）６個に分割する例を示して下さい。

（２）ｎを６以上の任意の整数とするとき、ｎ個の正三角形に必ず分割できることを説明して下さい。

２．解答例１(Ａｓａｍｉさん、ちゃめさん、たなかさん、吉田和義さん、kuri)

（設問１）

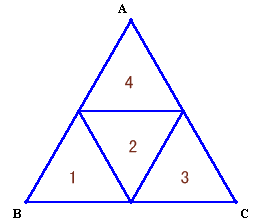
例えば、下図のように９等分した上４個分を１つの正三角形にすると６つの正三角形に分割することができます。

図１
参考図１

　

（設問２）

７、８分割の例を示します。

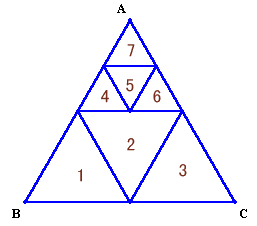
（１）７分割の例（図２）
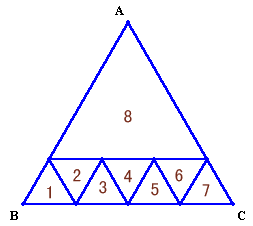
参考図２		 （２）８分割の例（図３）
参考図３

（３）ｎが６以上の任意の整数の場合

図２では４分割（問題図）した１つの正三角形を４分割することで、７分割（＋４−１＝＋３）が可能となっている。
同様にして、
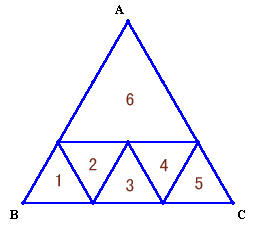
　　６分割（図１）から出発して６→９→１２→・・・（ｎ：３の倍数）
　　７分割（図２）から出発して７→１０→１３→・・・（ｎ：３で割った余り１）
　　８分割（図３）から出発して８→１１→１４→・・・（ｎ：３で割った余り２）
分割が可能。
従って、６以上の任意の整数ｎに対してｎ分割が可能となります。

以上

３．解答例２(ありさのお父さん、tomhさん、伊藤建志さん)

（設問１）省略。

（設問２）

図１，図３と同様にして、４以上の偶数個に分割できることを示します。

n≧2とし、正三角形をｎ2等分します。
すると、ｎ段ある各段には１，３，５，・・・、（２ｎ−１）個の正三角形があります。
このうち、最下段はそのままにして、残りの部分を１個の正三角形にまとめると（２ｎ−１）＋１＝２ｎ個の正三角形に分割されたことになります。

従って、４、６、８、１０、・・・等の偶数個に分割できることになります。

次に、２ｎ個に分割したもののうち、１個の正三角形をを４分割すると（２ｎ＋３）個に分割できます。

よって、７、９、１１、１３、・・・等の奇数個にも分割できることになります。

以上から、６以上の任意の整数個に分割できることが分かりました。