第14問の解答
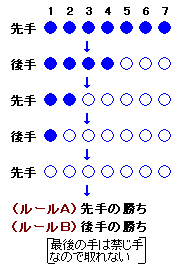
1.問題
 |
|
2.解答例1(清川育男さん、ちゃめさん、tomhさん、ありさのお父さん他)
(設問1)
結論からいうと、4の倍数、すなわち碁石の数が4個と8個のときが後手必勝になります。
- 1、2、3個のとき:
先手は全ての碁石を取ることができますので、先手必勝になります。 - 4個のとき:
先手が1、2、3個いずれの個数を取ったとしても、残り個数は3、2、1個となるので、後手は残りの碁石を全てを取ることが出来るので、後手必勝。 - 5、6、7個のとき:
先手は残り個数が4個となるように石を取ることができます。(5個のとき:1個、6個のとき:2個、7個のとき3個取る)
次は、後手の番ですが、残り個数が4個になったので、相手すなわち先手が必勝になります。 - 8個のとき:
先手が1、2、3個いずれの個数を取ったとしても、後手は残り個数は4個とすることができます。4個は後手必勝なので、結局8個も後手必勝。 - 9個のとき:
先手は1個取って残り8個に出来ます。
次は、後手の番ですが、残り個数が4個になったので、相手すなわち先手が必勝になります。
(設問2)
設問2も結論からいうと、設問1と同じ結果、4、8個が後手必勝になります。
- 1、2、3個のとき:設問1と同様先手必勝
- 4個のとき:
先手が1、3個取ったときは、設問1と同様に後手は残り全部を取れる。
先手が2個取ったときは、後手は2個が禁じ手なので1個しか取れない。
しかし、残った1個を先手は禁じ手のため取れなくなるので後手の勝ち。
結局、4個のときは設問1と同じ後手必勝となる。 - 5、6、7個のとき:先手は残りを4個とすることができる。
後手は、禁じ手のため手が狭まるだけで結果は、設問1と同様先手必勝 - 8個のとき:
先手が1、3個取ったときは、設問1と同様に後手は残り4個にできる。
先手が2個取ったときは、後手は2個が禁じ手なので1個しか取れない。
この時点で残りは5個。しかし、1個を先手は禁じ手のため取れなくなるので、先手は4個にすることはできず、3個以下にせざるを得ない。
先手が2個取ったときは残り3個、3個取ったときは残り2個。いずれも先手は残り全部取れるので、結局8個のときも設問1と同じ後手必勝となる。
- 9個のとき:設問1と同様に後手は1個取って残りを8個にできるので、先手必勝。
(補足)
先程の議論を整理すると、この問題では、取ることが出来る手が有限でかつ石の数が減る方向へ一方的に進むので、帰納法により次のようにして先手必勝か後手必勝かを求めていくことが出来ます。
- 先手が取ることの出来る手の結果が全て先手必勝のとき:後手必勝
- 先手が取る手の中に結果が後手必勝のものがあるとき: 先手必勝
さて、ルールBでは禁じ手がありますので、残った碁石の数だけでなく、相手が何個石を取ってその個数になったかも関係してきます。
(m個取ってn個残った状態を[n,m]と表すことにします)
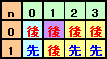
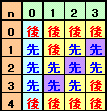
- 残り碁石が0個のとき:先手は取る石がもう無いので後手必勝とみなす。
- 残り碁石が1個のとき:
[1,0]、[1,2]、[1,3]:先手は1個取って[0,1]にできるので先手必勝
[1,1] :先手が1個取るのは禁じ手なので後手必勝
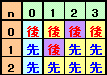
残り碁石が2個のとき:
[2,0]、[2,1]、[2,3]:先手は2個取って[0,2]にできるので先手必勝
[2,2] :先手は1個取って[1,1]にできるので先手必勝
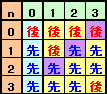
残り碁石が3個のとき:
[3,0]、[3,1]、[3,2]:先手は3個取って[0,3]にできるので先手必勝
[3,3] :先手の取れる[2,1]、[1,2]はいずれも先手必勝なので後手必勝
残り碁石が4個のとき:
[4,0]、[4,1]、[4,2]、[4,3] :
先手の取れる[3,1]、[2,2]、[1,3]はいずれも先手必勝なので後手必勝
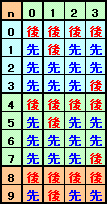
以下同様にして
残り碁石が4の倍数のとき:後手必勝
残り碁石が4の倍数以外のとき:先手必勝
以上